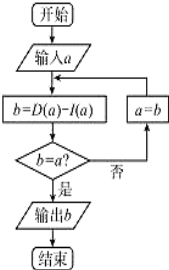
题目内容
【题目】设事件A表示“关于![]() 的一元二次方程
的一元二次方程![]() 有实根”,其中
有实根”,其中![]() ,
,![]() 为实常数.
为实常数.
(Ⅰ)若![]() 为区间[0,5]上的整数值随机数,
为区间[0,5]上的整数值随机数,![]() 为区间[0,2]上的整数值随机数,求事件A发生的概率;
为区间[0,2]上的整数值随机数,求事件A发生的概率;
(Ⅱ)若![]() 为区间[0,5]上的均匀随机数,
为区间[0,5]上的均匀随机数,![]() 为区间[0,2]上的均匀随机数,求事件A发生的概率.
为区间[0,2]上的均匀随机数,求事件A发生的概率.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】试题分析:
(1)列出所有可能的事件,结合古典概型公式可得满足题意的概率值为![]() ;
;
(2)利用题意画出概率空间,结合几何概型公式可得满足题意的概率值为![]() .
.
试题解析:
(Ⅰ)当a∈{0,1,2,3,4,5},b∈{0,1,2}时,共可以产生6×3=18个一元二次方程.
若事件A发生,则a 2-4b2≥0,即|a|≥2|b|. 又a≥0, b≥0,所以a≥2b.
从而数对(a,b)的取值为(0,0),(1,0),(2,0),(2,1),(3,0),(3,1),(4,0),(4,1),(4,2),(5,0),(5,1),(5,2),共12组值.
所以P(A)=![]() .
.
(Ⅱ)据题意,试验的全部结果所构成的区域为D={(a,b)|0≤a≤5,0≤b≤2},构成事件A的区域为A={(a,b)|0≤a≤5,0≤b≤2,a≥2b}.
在平面直角坐标系中画出区域A、D,如图,
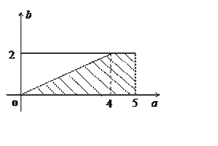
其中区域D为矩形,其面积S(D)=5×2=10,
区域A为直角梯形,其面积S(A)=![]() .
.
所以P(A)=![]() .
.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目