题目内容
下列关于函数f(x)=(2x-x2)ex的判断正确的是( )
①f(x)>0的解集是{x|0<x<2};
②f(-
)是极小值,f(
)是极大值;
③f(x)没有最小值,也没有最大值.
①f(x)>0的解集是{x|0<x<2};
②f(-
| 2 |
| 2 |
③f(x)没有最小值,也没有最大值.
| A、①③ | B、①②③ | C、② | D、①② |
分析:令f(x)>0可解x的范围确定①正确;
对函数f(x)进行求导,然后令f'(x)=0求出x,在根据f'(x)的正负判断原函数的单调性进而可确定②正确.
根据函数的单调性可判断极大值即是原函数的最大值,无最小值,③不正确.从而得到答案.
对函数f(x)进行求导,然后令f'(x)=0求出x,在根据f'(x)的正负判断原函数的单调性进而可确定②正确.
根据函数的单调性可判断极大值即是原函数的最大值,无最小值,③不正确.从而得到答案.
解答:解:由f(x)>0?(2x-x2)ex>0?2x-x2>0?0<x<2,故①正确;
f′(x)=ex(2-x2),由f′(x)=0得x=±
,
由f′(x)<0得x>
或x<-
,
由f′(x)>0得-
<x<
,
∴f(x)的单调减区间为(-∞,-
),(
,+∞).单调增区间为(-,
).
∴f(x)的极大值为f(
),极小值为f(-
),故②正确.
∵x<-
时,f(x)<0恒成立.
∴f(x)无最小值,但有最大值f(
)
∴③不正确.
故选D.
f′(x)=ex(2-x2),由f′(x)=0得x=±
| 2 |
由f′(x)<0得x>
| 2 |
| 2 |
由f′(x)>0得-
| 2 |
| 2 |
∴f(x)的单调减区间为(-∞,-
| 2 |
| 2 |
| 2 |
∴f(x)的极大值为f(
| 2 |
| 2 |
∵x<-
| 2 |
∴f(x)无最小值,但有最大值f(
| 2 |
∴③不正确.
故选D.
点评:本题主要考查函数的极值与其导函数关系,即函数取到极值时导函数一定等于0,但导函数等于0时还要判断原函数的单调性才能确定原函数的极值点.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
 12、已知函数f(x)的定义域为[-1,5],部分对应值如下表.
12、已知函数f(x)的定义域为[-1,5],部分对应值如下表.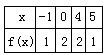
 已知函数f(x)的定义域为[-1,5],部分对应值如下表.f(x)的导函数y=f'(x)的图象如图所示.
已知函数f(x)的定义域为[-1,5],部分对应值如下表.f(x)的导函数y=f'(x)的图象如图所示.