题目内容
12、已知函数f（x）的定义域为[-1，5]，部分对应值如下表．
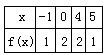
f（x）的导函数y=f'（x）的图象如图所示．
下列关于函数f（x）的命题：
①函数y=f（x）是周期函数；
②函数f（x）在[0，2]是减函数；
③如果当x∈[-1，t]时，f（x）的最大值是2，那么t的最大值为4；
④当1＜a＜2时，函数y=f（x）-a有4个零点．
其中真命题的个数是（ ）
分析：先由导函数的图象和原函数的关系画出原函数的大致图象，再借助与图象和导函数的图象，对四个命题，一一进行验证，对于假命题采用举反例的方法进行排除即可得到答案．
解答：解：由导函数的图象和原函数的关系得，原函数的大致图象如图：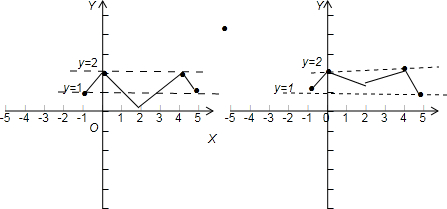
由图得：①为假命题，[-1，0]与[4，5]上单调性相反，但原函数图象不一定对称．
②为真命题．因为在[0，2]上导函数为负，故原函数递减；
③为假命题，当t=5时，也满足x∈[-1，t]时，f（x）的最大值是2；
④为假命题，当a离1非常接近时，对于第二个图，y=f（x）-a有2个零点，也可以是3个零点．
综上得：真命题只有②．
故选 D．
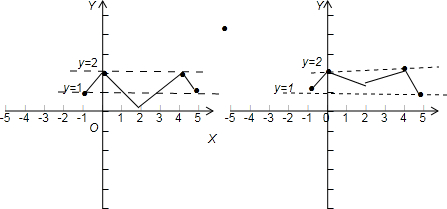
由图得：①为假命题，[-1，0]与[4，5]上单调性相反，但原函数图象不一定对称．
②为真命题．因为在[0，2]上导函数为负，故原函数递减；
③为假命题，当t=5时，也满足x∈[-1，t]时，f（x）的最大值是2；
④为假命题，当a离1非常接近时，对于第二个图，y=f（x）-a有2个零点，也可以是3个零点．
综上得：真命题只有②．
故选 D．
点评：本题主要考查导函数和原函数的单调性之间的关系．二者之间的关系是：导函数为正，原函数递增；导函数为负，原函数递减．
练习册系列答案
品学双优卷系列答案
小学期末冲刺100分系列答案
期末复习检测系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
