题目内容
【题目】在多面体![]() 中,底面
中,底面![]() 是梯形,四边形
是梯形,四边形![]() 是正方形,
是正方形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
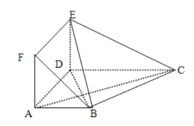
(1)求证:平面![]() 平面
平面![]() ;
;
(2)设![]() 为线段
为线段![]() 上一点,
上一点,![]() ,求二面角
,求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
【答案】(1)见解析;(2)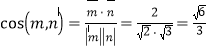 .
.
【解析】分析:(1)由勾股定理的逆定理可得![]() ,
,![]() ;又由条件可得到
;又由条件可得到![]() ,于是
,于是![]() 平面
平面![]() ,可得
,可得![]() ,从而得到
,从而得到![]() 平面
平面![]() ,根据面面垂直的判定定理得平面
,根据面面垂直的判定定理得平面![]() 平面
平面![]() .(2)由题意得可得
.(2)由题意得可得![]() ,
,![]() ,
,![]() 两两垂直,故可建立空间直角坐标系,结合题意可得点
两两垂直,故可建立空间直角坐标系,结合题意可得点![]() ,于是可求得平面
,于是可求得平面![]() 的法向量为
的法向量为![]() ,又
,又![]() 是平面
是平面![]() 的一个法向量,求得
的一个法向量,求得![]() 后结合图形可得所求余弦值为
后结合图形可得所求余弦值为![]() .
.
详解:(1)由![]() ,
,![]() ,
,![]() ,得
,得![]() ,
,
∴![]() 为直角三角形,且
为直角三角形,且![]()
同理![]() 为直角三角形,且
为直角三角形,且![]() .
.
又四边形![]() 是正方形,
是正方形,
∴![]() .
.
又![]()
∴![]() .
.
在梯形![]() 中,过点作
中,过点作![]() 作
作![]() 于
于![]() ,
,
故四边形![]() 是正方形,
是正方形,
∴![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
∴![]() ,
,
又![]() ,
,
∴![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
(2)由(1)可得![]() ,
,![]() ,
,![]() 两两垂直,以
两两垂直,以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 所在直线为
所在直线为![]() 轴建立如图所示的空间直角坐标系
轴建立如图所示的空间直角坐标系![]() ,
,
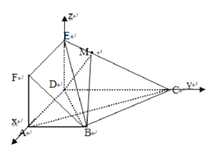
则![]() .
.
令![]() ,则
,则![]() ,
,![]()
∵![]() ,
,
∴![]()
∴点![]() .
.
∵![]() 平面
平面![]() ,
,
∴![]() 是平面
是平面![]() 的一个法向量.
的一个法向量.
设平面![]() 的法向量为
的法向量为![]() .
.
则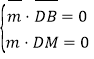 ,即
,即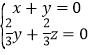 ,可得
,可得![]() .
.
令![]() ,得
,得![]() .
.
∴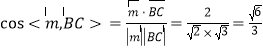 .
.
由图形知二面角![]() 为锐角,
为锐角,
∴二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]() .
.

【题目】某种仪器随着使用年限的增加,每年的维护费相应增加. 现对一批该仪器进行调查,得到这批仪器自购入使用之日起,前5年平均每台仪器每年的维护费用大致如下表:
年份 | 1 | 2 | 3 | 4 | 5 |
维护费 | 0.7 | 1.2 | 1.6 | 2.1 | 2.4 |
(1)根据表中所给数据,试建立![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若该仪器的价格是每台12万元,你认为应该使用满五年换一次仪器,还是应该使用满八年换一次仪器?并说明理由.
参考公式:用最小二乘法求线性回归方程![]() 的系数公式:
的系数公式:
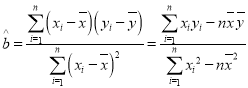 ,
,![]()
【题目】某厂生产不同规格的一种产品,根据检测标准,其合格产品的质量![]() 与尺寸x(mm)之间近似满足关系式
与尺寸x(mm)之间近似满足关系式![]() (b、c为大于0的常数).按照某项指标测定,当产品质量与尺寸的比在区间
(b、c为大于0的常数).按照某项指标测定,当产品质量与尺寸的比在区间![]() 内时为优等品.现随机抽取6件合格产品,测得数据如下:
内时为优等品.现随机抽取6件合格产品,测得数据如下:
尺寸x(mm) | 38 | 48 | 58 | 68 | 78 | 88 |
质量y (g) | 16.8 | 18.8 | 20.7 | 22.4 | 24 | 25.5 |
质量与尺寸的比 | 0.442 | 0.392 | 0.357 | 0.329 | 0.308 | 0.290 |
(Ⅰ)现从抽取的6件合格产品中再任选3件,记![]() 为取到优等品的件数,试求随机变量
为取到优等品的件数,试求随机变量![]() 的分布列和期望;
的分布列和期望;
(Ⅱ)根据测得数据作了初步处理,得相关统计量的值如下表:
|
|
|
|
75.3 | 24.6 | 18.3 | 101.4 |
(ⅰ)根据所给统计量,求y关于x的回归方程;
(ⅱ)已知优等品的收益![]() (单位:千元)与
(单位:千元)与![]() 的关系为
的关系为![]() ,则当优等品的尺寸x为何值时,收益
,则当优等品的尺寸x为何值时,收益![]() 的预报值最大?(精确到0.1)
的预报值最大?(精确到0.1)
附:对于样本![]()
![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: ,
,![]() ,
,![]() .
.
【题目】某糕点房推出一类新品蛋糕,该蛋糕的成本价为4元,售价为8元.受保质期的影响,当天没有销售完的部分只能销毁.经过长期的调研,统计了一下该新品的日需求量.现将近期一个月(30天)的需求量展示如下:
日需求量x(个) | 20 | 30 | 40 | 50 |
天数 | 5 | 10 | 10 | 5 |
(1)从这30天中任取两天,求两天的日需求量均为40个的概率.
(2)以上表中的频率作为概率,列出日需求量![]() 的分布列,并求该月的日需求量
的分布列,并求该月的日需求量![]() 的期望.
的期望.
(3)根据(2)中的分布列求得当该糕点房一天制作35个该类蛋糕时,对应的利润的期望值为![]() ;现有员工建议扩大生产一天45个,求利用利润的期望值判断此建议该不该被采纳.
;现有员工建议扩大生产一天45个,求利用利润的期望值判断此建议该不该被采纳.