题目内容
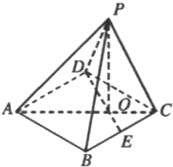 如图,已知四棱锥P-ABCD的底面的菱形,∠BCD=60°,点E是BC边的中点,AC与DE交于点O,PO⊥平面ABCD,
如图,已知四棱锥P-ABCD的底面的菱形,∠BCD=60°,点E是BC边的中点,AC与DE交于点O,PO⊥平面ABCD,(1)求证:PD⊥BC;
(2)若AB=6
| 3 |
| 2 |
(3)在(2)的条件下,求异面直线PB与DE所成角的余弦值.
分析:(1)连接DB,DE⊥BC而PO⊥平面ABCD,则OD是斜边PD在底面ABCD内的射影,根据三垂线定理可知PD⊥BC;
(2)根据二面角平面角的定义可知∠PDO为二面角P-AD-C的平面角,在Rt△POD中,求出∠PDO即可;
(3)取AD中点H,连接HB,HP则HB∥DE,HB与PB所成的角既是DE与PBD所成角,连接OH,OB,在Rt△DOH中,求出OH,在Rt△PHO中,求出PH,在Rt△POB中,求出PB,设HB与PB所成角为α,利用余弦定理可求出此角.
(2)根据二面角平面角的定义可知∠PDO为二面角P-AD-C的平面角,在Rt△POD中,求出∠PDO即可;
(3)取AD中点H,连接HB,HP则HB∥DE,HB与PB所成的角既是DE与PBD所成角,连接OH,OB,在Rt△DOH中,求出OH,在Rt△PHO中,求出PH,在Rt△POB中,求出PB,设HB与PB所成角为α,利用余弦定理可求出此角.
解答: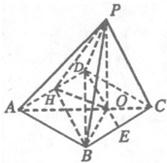 解:(1)证明:在菱形ABCD中,连接DB则△BCD是等边三角形.
解:(1)证明:在菱形ABCD中,连接DB则△BCD是等边三角形.
点E是BC边的中点
∴DE⊥BC
∵PO⊥平面ABCD
∴OD是斜边PD在底面ABCD内的射
∴PD⊥BC
(2)解:由(1)知DE⊥BC
菱形ABCD中AD∥BC∴DE⊥AD有∵PO⊥平面ABCD
DE是PD在平面ABCD的射影
∴PD⊥AD
∴PDO为二面角P-AD-C的平面角
菱形ABCD中,AD⊥DE
由(1)知△BCD为等边三角形
∵点E是BC边的中点AC与BD互相平分
∴点O是△BCD重心∵AB=
又∵在等边△BCD中,
DO=
DE=
BC=
•
=6
∴OC=OD=6∵PC=
∴PO=6
∴在Rt△POD中,tan∠PDO=
=
=1∴∠PDO=
∴二面角P-AD-C的大小为
(3)解:取AD中点H,连接HB,HP则HB∥DE
∴HB与PB所成的角既是DE与PBD所成角
连接OH,OB
∵PO⊥平面ABCD,OH,OB?平面ABCD
∴PO⊥OH,PO⊥OB
在Rt△DOH中,HD=3
OD=6
∴OH=3
在Rt△PHO中,PH=
=
在Rt△POB中,OB=OC=6,PB=
=6
由(2)可知DE=HB=9
设HB与PB所成角为α
则cosα=
=
异面直线PB,DE所成角的余弦值为
 解:(1)证明:在菱形ABCD中,连接DB则△BCD是等边三角形.
解:(1)证明:在菱形ABCD中,连接DB则△BCD是等边三角形.点E是BC边的中点
∴DE⊥BC
∵PO⊥平面ABCD
∴OD是斜边PD在底面ABCD内的射
∴PD⊥BC
(2)解:由(1)知DE⊥BC
菱形ABCD中AD∥BC∴DE⊥AD有∵PO⊥平面ABCD
DE是PD在平面ABCD的射影
∴PD⊥AD
∴PDO为二面角P-AD-C的平面角
菱形ABCD中,AD⊥DE
由(1)知△BCD为等边三角形
∵点E是BC边的中点AC与BD互相平分
∴点O是△BCD重心∵AB=
| 6 | 3 |
DO=
| 2 |
| 3 |
| 2 |
| 3 |
| ||
| 2 |
| ||
| 3 |
| 6 | 3 |
∴OC=OD=6∵PC=
| 6 | 2 |
∴在Rt△POD中,tan∠PDO=
| PO |
| DO |
| 6 |
| 6 |
| π |
| 4 |
∴二面角P-AD-C的大小为
| π |
| 4 |
(3)解:取AD中点H,连接HB,HP则HB∥DE
∴HB与PB所成的角既是DE与PBD所成角
连接OH,OB
∵PO⊥平面ABCD,OH,OB?平面ABCD
∴PO⊥OH,PO⊥OB
在Rt△DOH中,HD=3
| 3 |
∴OH=3
| 7 |
在Rt△PHO中,PH=
| PO2+OH2 |
| 99 |
在Rt△POB中,OB=OC=6,PB=
| PO2+OB2 |
| 2 |
由(2)可知DE=HB=9
设HB与PB所成角为α
则cosα=
| HB2+PB2-PH2 |
| 2HBPB |
| ||
| 4 |
异面直线PB,DE所成角的余弦值为
| ||
| 4 |
点评:求二面角,关键是构造出二面角的平面角,常用的方法有利用三垂线定理和通过求法向量的夹角,然后再将其转化为二面角的平面角.

练习册系列答案
相关题目
 如图:已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点,
如图:已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点, 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点. 如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=60°,PD⊥AD.点E是BC边上的中点.
如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=60°,PD⊥AD.点E是BC边上的中点. (2012•崇明县二模)如图,已知四棱锥P-ABCD的底面ABCD为正方形,PA⊥平面ABCD,E、F分别是BC,PC的中点,AB=2,AP=2.
(2012•崇明县二模)如图,已知四棱锥P-ABCD的底面ABCD为正方形,PA⊥平面ABCD,E、F分别是BC,PC的中点,AB=2,AP=2. (2012•吉林二模)如图,已知四棱锥P-ABCD的底面是正方形,PA⊥面ABCD,且PA=AD=2,点M,N分别在PD,PC上,
(2012•吉林二模)如图,已知四棱锥P-ABCD的底面是正方形,PA⊥面ABCD,且PA=AD=2,点M,N分别在PD,PC上,