题目内容
【题目】在圆 ![]() 上任取一点
上任取一点 ![]() ,点
,点 ![]() 在
在 ![]() 轴的正射影为点
轴的正射影为点 ![]() ,当点
,当点 ![]() 在圆上运动时,动点
在圆上运动时,动点 ![]() 满足
满足 ![]() ,动点
,动点 ![]() 形成的轨迹为曲线
形成的轨迹为曲线 ![]() .
.
(Ⅰ)求曲线 ![]() 的方程;
的方程;
(Ⅱ)点 ![]() 在曲线
在曲线 ![]() 上,过点
上,过点 ![]() 的直线
的直线 ![]() 交曲线
交曲线 ![]() 于
于 ![]() 两点,设直线
两点,设直线 ![]() 斜率为
斜率为 ![]() ,直线
,直线 ![]() 斜率为
斜率为 ![]() ,求证:
,求证: ![]() 为定值.
为定值.
【答案】解:(Ⅰ)设点 ![]() 坐标为
坐标为 ![]() , 点
, 点 ![]() 的坐标为
的坐标为 ![]() ,则
,则 ![]() ,
, ![]()
因为点 ![]() 在圆
在圆 ![]() ,所以
,所以 ![]() ①
①
把 ![]() ,
, ![]() 代入方程①,得
代入方程①,得 ![]() ,
,
所以曲线 ![]() 的方程为
的方程为 ![]() .
.
(Ⅱ)方法一:由题意知直线 ![]() 斜率不为0,设直线
斜率不为0,设直线 ![]() 方程为
方程为 ![]() ,
, ![]()
由 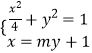 消去
消去 ![]() ,得
,得 ![]() ,
,
易知 ![]() ,得
,得 ![]()
![]()
![]() .所以
.所以 ![]() 为定值
为定值
方法二:(ⅰ)当直线 ![]() 斜率不存在时,
斜率不存在时, ![]()
所以 ![]()
(ⅱ)当直线 ![]() 斜率存在时,设直线
斜率存在时,设直线 ![]() 方程为
方程为 ![]() ,
, ![]()
由 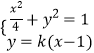 消去
消去 ![]() ,得
,得 ![]() ,
,
易知 ![]() ,
, ![]()
![]()
![]() .所以
.所以 ![]() 为定值
为定值
【解析】(I)用代入法求点的轨迹方程,设点 M 坐标为 ( x , y ) , 点 P 的坐标为 (![]() ,
, ![]() ),找到x,y与
),找到x,y与![]() 的关系即可。
的关系即可。
(II)此题结合直线与椭圆的位置关系,考察定值问题;因此设出直线的方程,联立,利用韦达定理得到点B、D的坐标的关系,再利用直线的斜率的坐标公式表示出![]() 即可。
即可。
【考点精析】解答此题的关键在于理解斜率的计算公式的相关知识,掌握给定两点P1(x1,y1),P2(x2,y2),x1≠x2,用两点的坐标来表示直线P1P2的斜率:斜率公式: k=y2-y1/x2-x1,以及对椭圆的标准方程的理解,了解椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() .
.

练习册系列答案
相关题目