题目内容
已知数列{an}满足a1=1，a2=3，且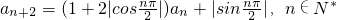
，
（1）求a2k-1（k∈N*）；
（2）数列{yn}，{bn}满足y=a2n-1，b1=y1，且当n≥2时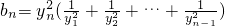
．证明当n≥2时，
；
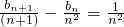（3）在（2）的条件下，试比较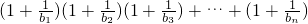
与4的大小关系．
解：（1）设n=2k-1
由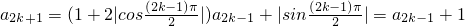
∴a2k+1-a2k-1=1
∴数列（a2k-1}为等差数列．
∴a2k-1=k（k∈N*）； …（4分）
（2）证：y=a2n-1=n．当n≥2时，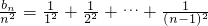
…①
∴
…②…（6分）
②式减①式，有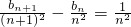
，得证． …（8分）
（3）解：当n=1时，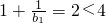
；
当n=2时，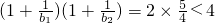
，
由（2）知，当n≥2时，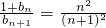
，
∴当n≥3时，=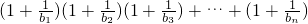
∵
，
∴
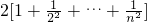
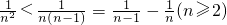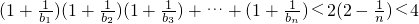…（14分）
分析：（1）设n=2k-1，利用条件可证数列（a2k-1}为等差数列．从而可求其通项；
（2）先求得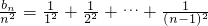，，然后再写一式，两式相减即可证得；
（3）先计算的当n=1时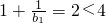，；当n=2时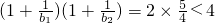，，再证当n≥3时，利用放缩法结合裂项求和即可的结论．
点评：本题以数列为载体，考查等差数列的定义，考查数列与不等式的结合，有较强的技巧性．
由
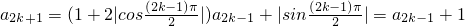
∴a2k+1-a2k-1=1
∴数列（a2k-1}为等差数列．
∴a2k-1=k（k∈N*）； …（4分）
（2）证：y=a2n-1=n．当n≥2时，
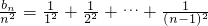…①∴
…②…（6分）②式减①式，有
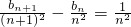，得证． …（8分）（3）解：当n=1时，
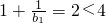；当n=2时，
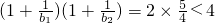，由（2）知，当n≥2时，
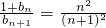，∴当n≥3时，
=∵
，∴
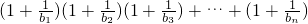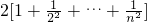
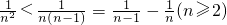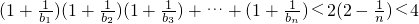…（14分）分析：（1）设n=2k-1，利用条件可证数列（a2k-1}为等差数列．从而可求其通项；
（2）先求得，
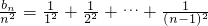，然后再写一式，两式相减即可证得；（3）先计算的当n=1时，
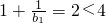；当n=2时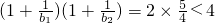，，再证当n≥3时，利用放缩法结合裂项求和即可的结论．点评：本题以数列为载体，考查等差数列的定义，考查数列与不等式的结合，有较强的技巧性．
练习册系列答案
相关题目