题目内容
(本小题满分14分)在平面直角坐标系中,已知点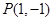 ,过点
,过点 作抛物线
作抛物线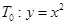 的切线,其切点分别为
的切线,其切点分别为 (其中
(其中 )。
)。
⑴ 求 的值;
的值;
⑵ 若以点 为圆心的圆与直线
为圆心的圆与直线 相切,求圆的面积。
相切,求圆的面积。
⑴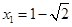 ,
,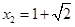 ;⑵圆的面积为
;⑵圆的面积为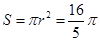 。
。
解析试题分析:(Ⅰ)由y=x2先求出y′=2x.再由直线PM与曲线T0相切,且过点P(1,-1),得到x1=1-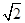 ,或x1=1+
,或x1=1+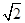 ;同理可得x2=1-
;同理可得x2=1-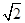 ,或x2=1+
,或x2=1+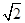 ,然后由x1<x2知x1=1-
,然后由x1<x2知x1=1-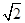 ,x2=1+
,x2=1+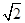 .
.
(Ⅱ)由题意知,x1+x2=2,x1•x2=-1,则直线MN的方程为:2x-y+1=0.再由点P到直线MN的距离即为圆E的半径,可求出圆E的面积.
解:⑴由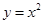 可得,
可得,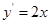 ……1分
……1分
∵直线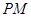 与曲线
与曲线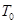 相切,且过点
相切,且过点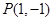 ,∴
,∴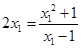 ,即
,即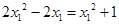 ,
,
即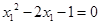 , ……3分 ∴
, ……3分 ∴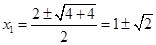 , ……5分
, ……5分
同理可得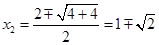 ……6分
……6分
∵ ∴
∴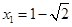 ,
,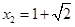 ……7分
……7分
⑵由⑴知,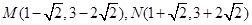
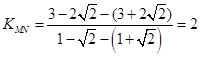 ……9分
……9分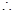 直线
直线 方程为:
方程为: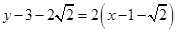 , 即
, 即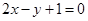 ……11分
……11分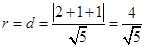 ……13分 故圆的面积为
……13分 故圆的面积为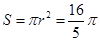 ……14分
……14分
考点:本试题主要考查了直线和圆锥曲线的位置关系,运用导数的思想得到切线的斜率,进而得到坐标的值,解题时要认真审题,仔细解答.
点评:解决该试题的关键是能运用导数的几何意义得到切点的坐标,并能利用韦达定理,得到直线方程,点到直线的距离公式得到圆的半径求解其面积。

练习册系列答案
相关题目
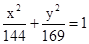 有共同焦点,且过点(0,2)的双曲线方程,并且求出这条双曲线的实轴长、焦距、离心率以及渐近线方程.
有共同焦点,且过点(0,2)的双曲线方程,并且求出这条双曲线的实轴长、焦距、离心率以及渐近线方程.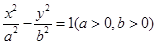 的一个焦点,并与双曲线的实轴垂直,已知抛物线与双曲线的交点为
的一个焦点,并与双曲线的实轴垂直,已知抛物线与双曲线的交点为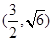 .
.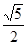 ,且与椭圆
,且与椭圆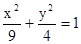 有公共焦点,
有公共焦点,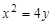 的焦点,且离心率等于
的焦点,且离心率等于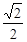 ,直线
,直线 与椭圆C交于M,N两点.
与椭圆C交于M,N两点.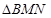 的垂心?若可以,求出直线
的垂心?若可以,求出直线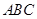 内有一动点
内有一动点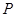 ,已知
,已知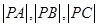 ,且满足
,且满足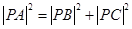 ,求
,求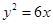 , 过点
, 过点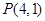 引一弦,使它恰在点
引一弦,使它恰在点 被平分,求这条弦所在的直线
被平分,求这条弦所在的直线 的方程.
的方程. 在y轴上的截距为m(m≠0),
在y轴上的截距为m(m≠0),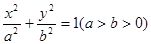 的左右焦点分别为
的左右焦点分别为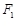 、
、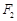 ,短轴两个端点为
,短轴两个端点为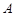 、
、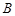 ,且四边形
,且四边形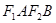 是边长为2的正方形。
是边长为2的正方形。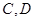 分别是椭圆长轴的左右端点,动点
分别是椭圆长轴的左右端点,动点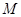 满足
满足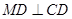 ,连接
,连接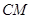 ,交椭圆于点
,交椭圆于点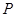 ;证明:
;证明: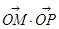 为定值;
为定值;