题目内容
18.函数y=loga(x-1)(其中a>0且a≠1)的图象恒过定点(2,0).分析 令y=loga(x-1)的真数值为1,求得自变量x的值即可求得答案.
解答 解:令x-1=1,得x=2,
∵f(2)=loga(2-1)=0,
∴函数f(x)=loga(x-1)的图象经过定点(2,0).
故答案为:(2,0).
点评 本题考查对数函数的单调性与特殊点,属于基础题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
9.已知f(x)是偶函数,它在[0,+∞)上是增函数,若f(lgx)>f(-1).则x的取值范围是( )
| A. | ($\frac{1}{10}$,1) | B. | (0,$\frac{1}{10}$)∪(10,+∞) | C. | ($\frac{1}{10}$,10) | D. | (0,1)∪(10,+∞) |
13.下列函数中,在各自定义域上既为增函数又为奇函数的是( )
| A. | f(x)=x|x| | B. | f(x)=x2+2 | C. | f(x)=2x-1 | D. | f(x)=-x3 |
3.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{x}+1,x<1}\\{lo{g}_{2}(x+1),x≥1}\end{array}\right.$,若f(a)=4,则实数a等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{4}{5}$ | C. | log23 | D. | 15 |
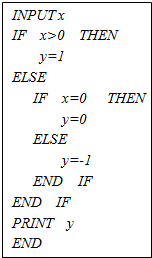 读程序,回答下列问题:
读程序,回答下列问题: