题目内容

7．已知复数（2k2-3k-2）+（k2-k）i在复平面内对应的点在第二象限．求实数k的取值范围．

分析 根据题意，列出不等式组$\left\{\begin{array}{l}{{2k}^{2}-3k-2＜0}\\{{k}^{2}-k＞0}\end{array}\right.$，求出解集即可．

解答 解：∵复数（2k2-3k-2）+（k2-k）i在复平面内对应的点在第二象限，
∴$\left\{\begin{array}{l}{{2k}^{2}-3k-2＜0}\\{{k}^{2}-k＞0}\end{array}\right.$，
解得$\left\{\begin{array}{l}{-\frac{1}{2}＜k＜2}\\{k＜0或k＞1}\end{array}\right.$，
即-$\frac{1}{2}$＜k＜0，或1＜k＜2；
∴实数k的取值范围是{k|-$\frac{1}{2}$＜k＜0，或1＜k＜2}．

点评 本题考查了复数的定义与应用问题，也考查了不等式组的解法与应用问题，是基础题目．

练习册系列答案
相关题目
17．已知$\overrightarrow{a}$=（2，-1），$\overrightarrow{b}$=（1，3），则（2$\overrightarrow{a}$-$\overrightarrow{b}$）•$\overrightarrow{a}$=11．
18．函数y=loga（x-1）（其中a＞0且a≠1）的图象恒过定点（2，0）．
15．a∈R，则“a=1”是“直线ax-y+2=0与直线x-ay-1=0平行”的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
2．求函数y=2${\;}^{\sqrt{-{x}^{2}+2x}}$的定义域、值域及单调增区间．
12．设x，y满足约束条件$\left\{\begin{array}{l}{2x-y+2≥0}\\{8x-y-4≤0}\\{x≥0，y≥0}\end{array}\right.$，若目标函数z=ax+by（a＞0，b＞0）的最大值为16，求ab的最大值．
19．记＜n＞表示正整数n的个位数，设Sn为数列{an}的前n项和，若an=＜n2＞，则Sn的值不可能为（　　）
A．4500B．4505C．4514D．4519
16．已知两点A（2，3）与B（4，5），且直线是线段AB的垂直平分线，圆的方程为x2+y2-2x-2y-$\frac{21}{2}$=0，解答下列问题：
（1）求直线的方程；
（2）判断直线与圆之间的位置关系，并说明理由．
17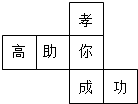．水平放置的正方体的六个面分别用“前面，后面，上面，下面，左面，右面”表示，如图是正方体的表面展开图，若图中“成”表示正方体的前面，“功”表示正方体的右面，“你”表示正方体的下面，则“孝”“高”“助”分别表示正方体的（　　）
A．左面，后面，上面B．后面，上面，左面C．上面，左面，后面D．后面，左面，上面

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网