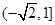题目内容
已知函数f(x)是定义在R上的奇函数,当x<0时,f(x)=ex(x+1),给出下列命题:
①当x>0时,f(x)=ex(1-x);②函数f(x)有两个零点;③f(x)>0的解集为(-1,0)∪(1,+∞);④?x1,x2∈R,都有|f(x1)-f(x2)|<2.
其中正确命题的个数是( )
| A.1 | B.2 |
| C.3 | D.4 |
B
解析

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
设 则a,b,c的大小关系为
则a,b,c的大小关系为
| A.a<c<b | B.b<a<c | C.a<b<c | D.b<c<a |
若定义在R上的函数f(x)满足f(-x)="f(x)," f(2-x)=f(x),且当x∈[0,1]时,其图象是四分之一圆(如图所示),则函数H(x)= |xex|-f(x)在区间[-3,1]上的零点个数为 ( )
| A.5 | B.4 | C.3 | D.2 |
已知 且
且 ,则
,则 ( )
( )
| A.有最大值2 | B.等于4 |
| C.有最小值3 | D.有最大值4 |
若|loga |=loga
|=loga ,|logba|=-logba,则a,b满足的条件是( )
,|logba|=-logba,则a,b满足的条件是( )
| A.a>1,b>1 | B.0<a<1,b>1 |
| C.a>1,0<b<1 | D.0<a<1,0<b<1 |
如图,A,B,C,D是某煤矿的四个采煤点,m是公路,图中所标线段为道路,ABQP,BCRQ,CDSR近似于正方形.已知A,B,C,D四个采煤点每天的采煤量之比约为5∶1∶2∶3,运煤的费用与运煤的路程、所运煤的质量都成正比.现要从P,Q,R,S中选出一处设立一个运煤中转站,使四个采煤点的煤运到中转站的费用最少,则地点应选在( )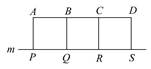
| A.P点 | B.Q点 | C.R点 | D.S点 |
方程lnx=6-2x的根必定属于区间( )
| A.(-2,1) | B.( ,4) ,4) |
C.(1, ) ) | D.( , , ) ) |
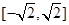 B.
B. 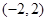 C.
C. 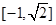 D.
D.