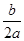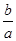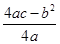题目内容
设 则a,b,c的大小关系为
则a,b,c的大小关系为
| A.a<c<b | B.b<a<c | C.a<b<c | D.b<c<a |
B
解析试题分析:因为 所以显然
所以显然 ,所以
,所以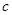 的值最大.故排除A,D选项.又因为
的值最大.故排除A,D选项.又因为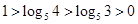 ,所以
,所以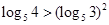 .即
.即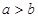 .综上
.综上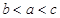 .故选B.本小题关键是进行对数的运算.
.故选B.本小题关键是进行对数的运算.
考点:1.对数的运算.2.数的大小比较的方法.

练习册系列答案
相关题目
设a>0,将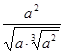 表示成分数指数幂,其结果是( )
表示成分数指数幂,其结果是( )
A.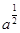 | B.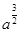 | C. | D. |
三个数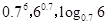 的大小关系为( )
的大小关系为( )
A.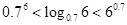 | B.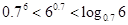 |
C.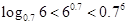 | D.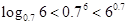 |
已知函数 ,若存在
,若存在 使得函数
使得函数 的值域是
的值域是 ,则实数
,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
已知函数f(x)=ax2+bx+c(a≠0),且f(x)=2x没有实数根,那么f(f(x))=4x的实根个数为( )
| A.0 | B.1 | C.2 | D.4 |
已知函数f(x)=x2-2(a+2)x+a2,g(x)=-x2+2(a-2)x-a2+8.设H1(x)=max{f(x),g(x)},H2(x)=min{f(x),g(x)}(max{p,q}表示p,q中的较大值,min{p,q}表示p,q中的较小值).记H1(x)的最小值为A,H2(x)的最大值为B,则A-B=( )
| A.16 | B.-16 |
| C.a2-2a-16 | D.a2+2a-16 |
若函数f(x)= 则f(f(10))=( )
则f(f(10))=( )
| A.lg101 | B.2 | C.1 | D.0 |