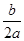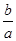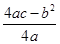题目内容
设函数f(x)的定义域为D,若存在非零实数l使得对于任意x∈M(M⊆D)有x+l∈D,且f(x+l)≥f(x),则称f(x)为M上的l高调函数,如果定义域为R的函数f(x)是奇函数,当x≥0时,f(x)=|x-a2|-a2,且f(x)为R上的8高调函数,那么实数a的取值范围是( )
A. 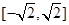 B.
B. 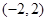 C.
C. 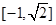 D.
D. 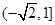
A
解析试题分析:当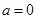 时,
时,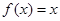 ,则
,则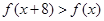 ,即
,即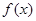 为
为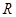 上的8高调函数;当
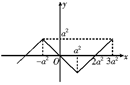
上的8高调函数;当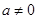 时,函数
时,函数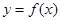 的图象如图所示,若
的图象如图所示,若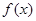 为
为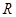 上的8高调函数,则
上的8高调函数,则 ,解得
,解得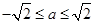 且
且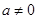 .综上
.综上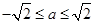 .
.
考点:1.新定义题;2.函数图像.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
已知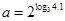 ,
,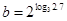 ,
,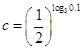 则
则
| A.a>b>c | B.b>a>c | C.a>c>b | D.c>a>b |
设a>0,将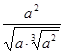 表示成分数指数幂,其结果是( )
表示成分数指数幂,其结果是( )
A.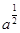 | B.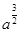 | C. | D. |
设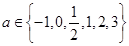 ,则使函数
,则使函数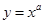 的定义域为R且为奇函数的所有
的定义域为R且为奇函数的所有 的值有( )
的值有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
若 ,则有( ).
,则有( ).
A.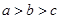 | B. | C. | D.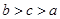 |
已知函数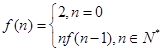 ,则
,则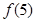 的值是( )
的值是( )
| A.4 | B.48 | C.240 | D.1440 |
已知函数f(x)=ax2+bx+c(a≠0),且f(x)=2x没有实数根,那么f(f(x))=4x的实根个数为( )
| A.0 | B.1 | C.2 | D.4 |