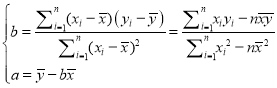题目内容
【题目】已知函数![]() .
.
(Ⅰ)若![]() ,求
,求![]() 在
在![]() 处的切线方程;
处的切线方程;
(Ⅱ)若![]() 对任意
对任意![]() 均有
均有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)求证:![]() .
.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)证明见解析.
;(Ⅲ)证明见解析.
【解析】
(Ⅰ)根据导数的几何意义求得斜率后,利用点斜式即可得解;
(Ⅱ)先求导,根据![]() 、
、![]() 分类讨论函数单调性,结合
分类讨论函数单调性,结合![]() 即可得解;
即可得解;
(Ⅲ)由(Ⅱ)知当![]() 时,
时,![]() ,转化可得
,转化可得![]() ,进而可得
,进而可得![]() ,即可得证.
,即可得证.
(Ⅰ)当![]() 时,
时,![]() ,则
,则![]() ,所以
,所以![]() ,
,
所以切线方程为![]() 即
即![]() ;
;
(Ⅱ)由题意![]() ,
,
令![]() ,则
,则![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 时恒成立;
时恒成立;
当![]() 时,
时,![]() 图象的对称轴为
图象的对称轴为![]() ,由
,由![]() 、
、![]() 可得
可得![]() 在
在![]() 时恒成立;
时恒成立;
所以当![]() 时,函数
时,函数![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() ,符合题意;
,符合题意;
当![]() 时,
时,![]() ,
,![]() ,
,![]() 图象的对称轴
图象的对称轴![]() ,
,
所以存在![]() ,使得
,使得![]() ,
,
则当![]() 时,
时,![]() 即
即![]() ,函数
,函数![]() 单调递增,
单调递增,
此时![]() ,不合题意.
,不合题意.
故所求实数![]() 的取值范围为
的取值范围为![]() ;
;
(Ⅲ)证明:由(Ⅱ)知,当![]() 时,函数
时,函数![]() 在
在![]() 单调递减,
单调递减,![]() ,
,
易知当![]() 时,
时,![]() 即
即![]() ,
,
所以![]() 即
即![]() ,所以
,所以 ,
,
令![]() ,则
,则![]() ,
,
所以![]() ,得证.
,得证.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某学习小组通过对某商场一种品牌服装销售情况的调查发现:该服装在过去的一个月内(以![]() 天计),日销售量
天计),日销售量 ![]() (件)与时间x (天)的部分数据如下表所示,给出以下四种函数模型:①
(件)与时间x (天)的部分数据如下表所示,给出以下四种函数模型:① ![]() ,②
,② ![]() ,③
,③ ![]() ④
④![]() .请你根据上表中的数据,从中选择你认为最合适的一种函数来描述日销售量
.请你根据上表中的数据,从中选择你认为最合适的一种函数来描述日销售量![]() (件)与时间x(天)的变化关系,请将你选择的函数序号填写在横线上__________.(不需要求出具体解析式)
(件)与时间x(天)的变化关系,请将你选择的函数序号填写在横线上__________.(不需要求出具体解析式)
x (天) | 10 | 20 | 25 | 30 |
| 110 | 120 | 125 | 120 |
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量![]() (吨)与相应的生产能耗
(吨)与相应的生产能耗![]() (吨)标准煤的几组对照数据
(吨)标准煤的几组对照数据
|
|
|
|
|
|
|
|
|
|
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
参考公式: