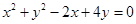题目内容
几何证明选讲如图:已知圆上的弧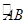 =
=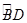 ,过C点的圆的切线与BA的延长线交于E点
,过C点的圆的切线与BA的延长线交于E点
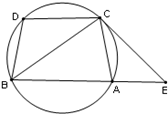
证明:(Ⅰ)∠ACE=∠BCD.(Ⅱ)BC2=BE×CD.
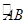 =
=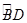 ,过C点的圆的切线与BA的延长线交于E点
,过C点的圆的切线与BA的延长线交于E点
证明:(Ⅰ)∠ACE=∠BCD.(Ⅱ)BC2=BE×CD.
由同圆中等圆弧的性质可得∠ABC=∠BCD.由弦切角定理可得∠ACE=∠ABC,即可得出证明.(II)利用弦切角定理可得∠CDB=∠BCE,由相似三角形的判定定理可得△BEC∽△CBD,由相似三角形的性质可得BC2=BE×CD.,即可求出BC
试题分析:解:(Ⅰ)因为
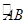 =
=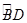 ,
,所以∠BCD=∠ABC.
又因为EC与圆相切于点C,
故∠ACE=∠ABC
所以∠ACE=∠BCD.(5分)
(Ⅱ)因为∠ECB=∠CDB,∠EBC=∠BCD,
所以△BDC~△ECB,
故BC:BE="CD:BC" .
即BC2=BE×CD.(10分)
点评:熟练掌握同圆中等圆弧的性质、弦切角定理、相似三角形的判定和性质定理是解题的关键.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
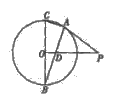
 与圆
与圆 相切于点
相切于点 ,直径
,直径  ,连结
,连结 交
交 于点
于点 .
.
 ;
;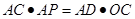 .
. 截圆x2+y2=4得的劣弧所对的圆心角是( )
截圆x2+y2=4得的劣弧所对的圆心角是( )



 经过坐标原点和点
经过坐标原点和点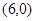 ,且与直线
,且与直线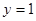 相切, 从圆
相切, 从圆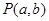 向该圆引切线
向该圆引切线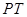 ,
,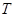 为切点,
为切点,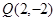 ,且
,且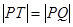 , 试判断点
, 试判断点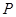 是否总在某一定直线
是否总在某一定直线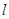 上,若是,求出
上,若是,求出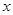 轴的交点为
轴的交点为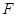 ,点
,点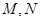 是直线
是直线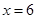 上两动点,且以
上两动点,且以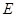 过点
过点 是⊙
是⊙ 的直径,
的直径,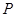 是
是 ,
, ,若
,若 ,则⊙
,则⊙

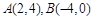 ,则以
,则以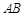 为直径的圆的方程是( )
为直径的圆的方程是( )



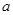 为任意实数时,直线
为任意实数时,直线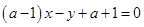 恒过定点
恒过定点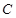 ,则以
,则以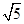 的圆是( )
的圆是( )