题目内容
(本题满分12分)
求圆心在直线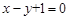 上,且经过圆
上,且经过圆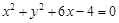 与圆
与圆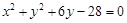 的交点的圆方程.
的交点的圆方程.
求圆心在直线
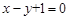 上,且经过圆
上,且经过圆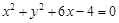 与圆
与圆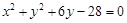 的交点的圆方程.
的交点的圆方程.(x+2)2 +(y+1)2 =17
试题分析:解析:设圆
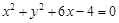 与圆
与圆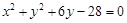 的交点为A、B,解方程组:
的交点为A、B,解方程组: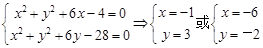
所以A(-1,3)、B(-6,-2)
因此直线AB的垂直平分线方程为:x+y+3=0
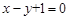 与x+y+3=0联立,解得:x=-2,y=-1,即:所求圆心C为(-2,-1)
与x+y+3=0联立,解得:x=-2,y=-1,即:所求圆心C为(-2,-1)半径r=AC=
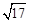 .
.故所求圆C的方程为:(x+2)2 +(y+1)2 =17
点评:求解圆的方程的关键是确定圆心和半径,然后得到标准方程,属于基础题。

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
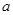 为任意实数时,直线
为任意实数时,直线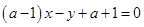 恒过定点
恒过定点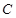 ,则以
,则以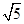 的圆是( )
的圆是( )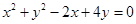





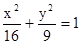 上一点, F1、F2是其焦点, 若∠F1P F2=90°, △F1P F2面积为 .
上一点, F1、F2是其焦点, 若∠F1P F2=90°, △F1P F2面积为 .  与直线
与直线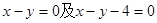 都相切,圆心在直线
都相切,圆心在直线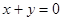 上,则圆
上,则圆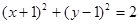

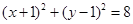
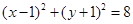
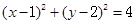 关于
关于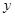 轴对称的圆的方程为______________.
轴对称的圆的方程为______________.  ,若线段
,若线段 是△
是△ 外接圆的直径,则点
外接圆的直径,则点 的坐标是( ).
的坐标是( ).