��Ŀ����
����Ŀ��ij�����̼ƻ���Ӫһ����Ʒ�����г����鷢�֣�����Ʒÿ�յ�������y����λ��ǧ�ˣ������ۼ۸�x����λ��Ԫ/ǧ�ˣ�1��x��12�����㣺��1��x��4ʱ��y=a��x��3��2+ ![]() ����a��bΪ����������4��x��12ʱ��y=
����a��bΪ����������4��x��12ʱ��y= ![]() ��100����֪�����ۼ۸�Ϊ2Ԫ/ǧ��ʱ��ÿ�տ��۳����ز�800ǧ�ˣ������ۼ۸�Ϊ3Ԫ/ǧ��ʱ��ÿ�տ��۳�150ǧ�ˣ�
��100����֪�����ۼ۸�Ϊ2Ԫ/ǧ��ʱ��ÿ�տ��۳����ز�800ǧ�ˣ������ۼ۸�Ϊ3Ԫ/ǧ��ʱ��ÿ�տ��۳�150ǧ�ˣ�
��1����a��b��ֵ����ȷ��y����x�ĺ�������ʽ��
��2��������Ʒ�����۳ɱ�Ϊ1Ԫ/ǧ�ˣ���ȷ�����ۼ۸�x��ֵ��ʹ����ÿ�����۸��ز���������f��x����� ![]() ��2.65��
��2.65��
���𰸡�
��1���⣺�����⣺
x=2ʱy=800����a+b=800��
�֡�x=3ʱy=150����b=300���ɵ�a=500
��y= 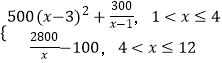
��2���⣺�����⣺
f��x��=y��x��1��=  ��
��
��1��x��4ʱ��
f��x��=500��x��3��2��x��1��+300=500x3��3500x2+7500x��4200��
f'��x��=500��3x��5����x��3����
����f�䣨x����0���� ![]() ��x��3��
��x��3��
��f��x���ڣ�1�� ![]() ������3��4���ϵ������ڣ�
������3��4���ϵ������ڣ� ![]() ��3���ϵݼ���
��3���ϵݼ���
��f�� ![]() ��=
��= ![]() +450��f��4��=1800��
+450��f��4��=1800��
�൱x=4ʱʱ�����ֵ��f��4��=1800
��4��x��12ʱ��
f��x��=�� ![]() ��100����x��1��=2900����100x+
��100����x��1��=2900����100x+ ![]() ����2900��400
����2900��400 ![]() ��1840��
��1840��
���ҽ���100x= ![]() ����x=2
����x=2 ![]() ��5.3ʱȡ�Ⱥţ�
��5.3ʱȡ�Ⱥţ�
��x=5.3ʱ�����ֵ1840��
��1800��1840��
�൱x=5.3ʱf��x�������ֵ1840
�������ۼ۸�Ϊ5.3Ԫ��ֵ��ʹ���������������
����������1��������֪�������뺯������ʽ�õ����������鼴�ɽ��δ֪����ֵ���õ������ķ��̡���2�����õ�����������ֵ��������һ�����ı亯�������Եĺ�����������㣬�ڵó��������������Ӧע���϶������������ʵ���������ֵ���⡣