题目内容
如果函数f(x)=x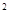 +bx+c对于任意实数t,都有f(2+t)=f(2-t),那么( )
+bx+c对于任意实数t,都有f(2+t)=f(2-t),那么( )
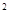 +bx+c对于任意实数t,都有f(2+t)=f(2-t),那么( )
+bx+c对于任意实数t,都有f(2+t)=f(2-t),那么( )| A.f(2)<f(1)<f(4) | B.f(1)<f(2)<f(4) |
| C.f(2)<f(4)<f(1) | D.f(4)<f(2)<f(1) |
A
试题分析:先从条件“对任意实数t都有f (2+t)=f (2-t)”得到对称轴,然后结合图象判定函数值的大小关系即可.解:∵对任意实数t都有f (2+t)=f (2-t)∴f(x)的对称轴为x=2,而f(x)是开口向上的二次函数故可画图观察可得f(2)<f(1)<f(4),故选A.
点评:本题考查了二次函数的图象,通过图象比较函数值的大小,数形结合有助于我们的解题,形象直观

练习册系列答案
相关题目
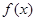 是二次函数,不等式
是二次函数,不等式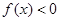 的解集是
的解集是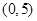 ,且
,且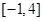 上的最大值为12.
上的最大值为12.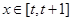 上的最小值为
上的最小值为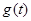 ,求
,求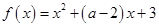 在区间
在区间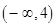 上是减函数,则a的取值范围是( ).
上是减函数,则a的取值范围是( ). 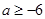 B.
B.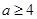 C
C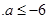 D.
D.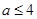
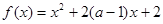 在区间
在区间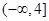 上递减,则实数
上递减,则实数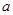 的取值范围是___
的取值范围是___  在
在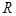 上满足
上满足 恒成立,则
恒成立,则 的取值范围
的取值范围 时,函数
时,函数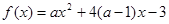 在
在 时取得最大值,则
时取得最大值,则 的取值范围是( )
的取值范围是( )
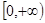


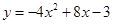 ,
,