题目内容
已知圆C的圆心在坐标原点,且过点M(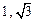 ).
).
(1)求圆C的方程;
(2)已知点P是圆C上的动点,试求点P到直线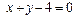 的距离的最小值;
的距离的最小值;
(3)若直线l与圆C相切,且l与x,y轴的正半轴分别相交于A,B两点,求△ABC的面积最小时直线
l的方程.
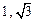 ).
).(1)求圆C的方程;
(2)已知点P是圆C上的动点,试求点P到直线
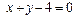 的距离的最小值;
的距离的最小值;(3)若直线l与圆C相切,且l与x,y轴的正半轴分别相交于A,B两点,求△ABC的面积最小时直线
l的方程.
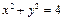 ,
,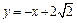
解析:(1)圆C的半径为
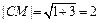 , ……………………… 2分
, ……………………… 2分所以圆C的方程为
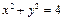 ………………………………………………………………3分
………………………………………………………………3分(2)圆心到直线l的距离为
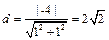 ,…………………………………………4分
,…………………………………………4分所以P到直线l:
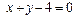 的距离的最小值为:
的距离的最小值为: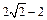 …………………………… 6分
…………………………… 6分(3)设直线l的方程为:
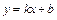 ,因为l与x,y轴的正半轴分别相交于A,B两点,则
,因为l与x,y轴的正半轴分别相交于A,B两点,则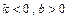 ,
,且
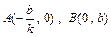 ,又l与圆C相切,则C点到直线l的距离等于圆的半径2,
,又l与圆C相切,则C点到直线l的距离等于圆的半径2,即:
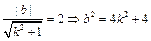 , ①, 而
, ①, 而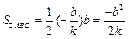 ② ……………… 8分
② ……………… 8分将①代入②得
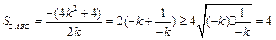 ,当且仅当k=﹣1时取等号,所以当k=﹣1时,△ABC的面积最小,此时
,当且仅当k=﹣1时取等号,所以当k=﹣1时,△ABC的面积最小,此时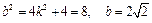 ,直线l的方程为:
,直线l的方程为: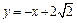 ……………… 10分
……………… 10分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
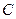 过点
过点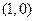 ,且圆心在
,且圆心在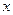 轴的正半轴上,直线
轴的正半轴上,直线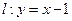 被该圆所截得的弦长为
被该圆所截得的弦长为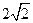 ,则圆
,则圆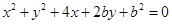 与x轴相切,则b的值为
与x轴相切,则b的值为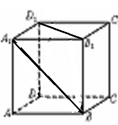
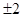
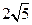
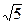
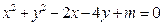 ,若此方程表示圆
,若此方程表示圆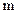 的取值范围
的取值范围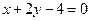 相交于M、N两点,且OM
相交于M、N两点,且OM ON
ON 知直线
知直线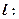
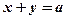 与圆
与圆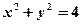 交于
交于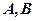 两点,且
两点,且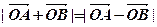 (其中O为坐标原点),则实数
(其中O为坐标原点),则实数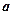 的值是 ( )
的值是 ( )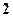
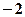
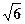 或
或