题目内容
(本小题满分16分)设数列 的前n项和为
的前n项和为 ,数列
,数列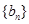 满足:
满足: 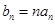 ,且数列
,且数列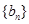 的前
的前
n项和为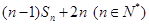 .
.
(1) 求 的值;
的值;
(2) 求证:数列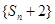 是等比数列;
是等比数列;
(3) 抽去数列 中的第1项,第4项,第7项,……,第3n-2项,……余下的项顺序不变,组成一个新数列
中的第1项,第4项,第7项,……,第3n-2项,……余下的项顺序不变,组成一个新数列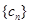 ,若
,若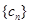 的前n项和为
的前n项和为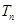 ,求证:
,求证: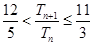 .
.
【答案】
解:(1)由题意得: 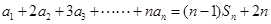 ;………………1分
;………………1分
当n=1时,则有: 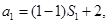 解得:
解得:  ;
;
当n=2时,则有: 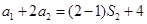 ,即
,即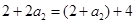 ,解得:
,解得: 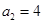 ;
;
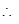
 ………………2分
………………2分
(2) 由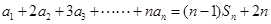 ① 得:
① 得:
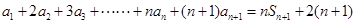 ②
………………3分
②
………………3分
② - ①得: 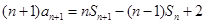 ,
,
即: 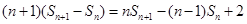 即:
即: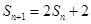 ;
……………5分
;
……………5分
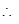
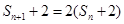 ,由
,由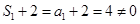 知:
知:
数列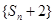 是以4为首项,2为公比的等比数列.…………………………………8分
是以4为首项,2为公比的等比数列.…………………………………8分
(3)由(2)知:  ,即
,即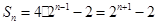 ……………………9分
……………………9分
当n≥2时,  对n=1也成立,
对n=1也成立,
即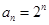 (n
(n ………………………………………………………….…10分
………………………………………………………….…10分
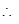 数列
数列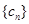 为
为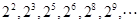 ,它的奇数项组成以4为首项、公比为8的等比数列;偶数项组成以8为首项、公比为8的等比数列;…………………11分
,它的奇数项组成以4为首项、公比为8的等比数列;偶数项组成以8为首项、公比为8的等比数列;…………………11分
 当n=2k-1
当n=2k-1 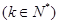 时,
时,
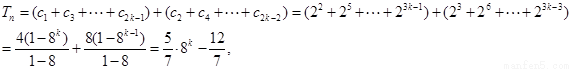
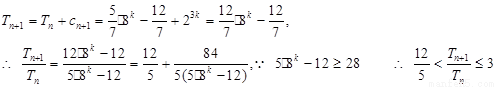 …………………14分
…………………14分
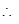 当n=2k
当n=2k 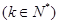 时,
时,
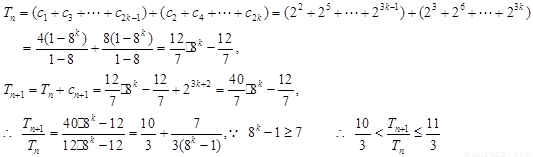
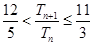 .……………………………………………………………16分
.……………………………………………………………16分
【解析】略

练习册系列答案
 能力评价系列答案
能力评价系列答案
相关题目
 在平面直角坐标系
在平面直角坐标系 ,
, (
( ),
),
 ,对任意
,对任意 时,
时, 恒成立,求实数
恒成立,求实数 的范围;
的范围; ,当“
,当“ 在
在 的最大值.
的最大值. :方程
:方程 无实数根;
命题
无实数根;
命题 :函数
:函数 的值域是
的值域是 .如果命题
.如果命题 为真命题,
为真命题, 为假命题,求实数
为假命题,求实数 的取值范围.
的取值范围. 为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
 )的值;
)的值; 个单位后,再将得到的图象上各点的横坐标延长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
个单位后,再将得到的图象上各点的横坐标延长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.