题目内容
方程log2x=x-3的实数解的个数为
2
2
.分析:本题即求函数y=log2x 与直线y=x-3 的交点的个数,数形结合可得结论.
解答:解:方程log2x=x-3的实数解的个数,即函数y=log2x 与直线y=x-3的交点的个数,如图所示:
结合图象可得函数y=log2x 与直线y=x-3 的交点的个数为2,
故答案为 2.
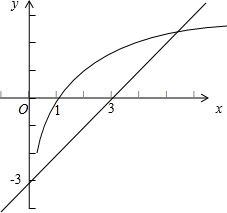
结合图象可得函数y=log2x 与直线y=x-3 的交点的个数为2,
故答案为 2.
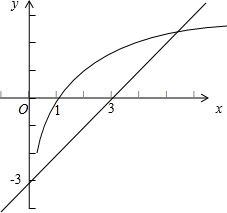
点评:本题考查函数的零点与方程的根的关系,考查作图能力,转化思想的应用,属于中档题.

练习册系列答案
相关题目
设方程2x+x+2=0和方程log2x+x+2=0的根分别为p和q,函数f(x)=(x+p)(x+q)+2,则( )
| A、f(2)=f(0)<f(3) | B、f(0)<f(2)<f(3) | C、f(3)<f(0)=f(2) | D、f(0)<f(3)<f(2) |