题目内容
设方程2x+x+2=0和方程log2x+x+2=0的根分别为p和q,函数f(x)=(x+p)(x+q)+2,则( )
| A、f(2)=f(0)<f(3) | B、f(0)<f(2)<f(3) | C、f(3)<f(0)=f(2) | D、f(0)<f(3)<f(2) |
分析:把两个方程分别看作指数函数与直线y=-x-2的交点B和对数函数与直线y=-x-2的交点A的横坐标分别为p和q,而指数函数与对数函数互为反函数则关于y=x对称,求出AB的中点坐标得到p+q=-2;然后把函数f(x)化简后得到一个二次函数,对称轴为直线x=-
=1,所以得到f(2)=f(0)且根据二次函数的增减性得到f(2)和f(0)都小于f(3)得到答案.
| p+q |
| 2 |
解答: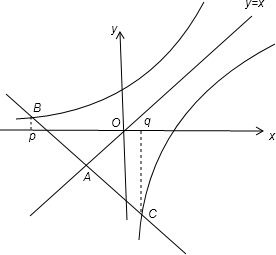 解:方程2x+x+2=0和方程log2x+x+2=0可以分别看作方程方程2x=-x-2和方程log2x=-x-2,方程2x+x+2=0和方程log2x+x+2=0的根分别为p和q即分别为函数y=2x与函数y=-x-2的交点B横坐标为p;y=log2x与y=-x-2的交点C横坐标为q.由y=2x与y=log2x互为反函数且关于y=x对称,所以BC的中点A一定在直线y=x上,联立得
解:方程2x+x+2=0和方程log2x+x+2=0可以分别看作方程方程2x=-x-2和方程log2x=-x-2,方程2x+x+2=0和方程log2x+x+2=0的根分别为p和q即分别为函数y=2x与函数y=-x-2的交点B横坐标为p;y=log2x与y=-x-2的交点C横坐标为q.由y=2x与y=log2x互为反函数且关于y=x对称,所以BC的中点A一定在直线y=x上,联立得
解得A点坐标为(-1,-1)根据中点坐标公式得到
=-1即p+q=-2,
则f(x)=(x+p)(x+q)+2=x2+(p+q)x+pq+2为开口向上的抛物线,且对称轴为x=-
=1,
得到f(0)=f(2)且当x>1时,函数为增函数,所以f(3)>f(2),
综上,f(3)>f(2)=f(0)
故选A
 解:方程2x+x+2=0和方程log2x+x+2=0可以分别看作方程方程2x=-x-2和方程log2x=-x-2,方程2x+x+2=0和方程log2x+x+2=0的根分别为p和q即分别为函数y=2x与函数y=-x-2的交点B横坐标为p;y=log2x与y=-x-2的交点C横坐标为q.由y=2x与y=log2x互为反函数且关于y=x对称,所以BC的中点A一定在直线y=x上,联立得
解:方程2x+x+2=0和方程log2x+x+2=0可以分别看作方程方程2x=-x-2和方程log2x=-x-2,方程2x+x+2=0和方程log2x+x+2=0的根分别为p和q即分别为函数y=2x与函数y=-x-2的交点B横坐标为p;y=log2x与y=-x-2的交点C横坐标为q.由y=2x与y=log2x互为反函数且关于y=x对称,所以BC的中点A一定在直线y=x上,联立得
|
| p+q |
| 2 |
则f(x)=(x+p)(x+q)+2=x2+(p+q)x+pq+2为开口向上的抛物线,且对称轴为x=-
| p+q |
| 2 |
得到f(0)=f(2)且当x>1时,函数为增函数,所以f(3)>f(2),
综上,f(3)>f(2)=f(0)
故选A
点评:此题是一道综合题,考查学生灵活运用指数函数、对数函数的图象与性质,要求学生掌握反函数的性质,会利用二次函数的图象与性质解决实际问题.

练习册系列答案
相关题目