题目内容
设α,β分别是关于x的方程log2x+x-4=0和2x+x-4=0的根,则α+β=分析:分别作出函数y=log2x,y=2x,y=4-x的图象相交于点P,Q.利用log2α=4-α,2β=4-β.而y=log2x(x>0)与y=2x互为反函数,直线y=4-x与直线y=x互相垂直,
点P与Q关于直线y=x对称.即可得出.
点P与Q关于直线y=x对称.即可得出.
解答:解:分别作出函数y=log2x,y=2x,y=4-x的图象,相交于点P,Q.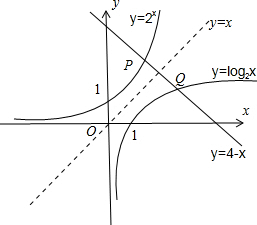
∵log2α=4-α,2β=4-β.
而y=log2x(x>0)与y=2x互为反函数,直线y=4-x与直线y=x互相垂直,
∴点P与Q关于直线y=x对称.
∴α=2β=4-β.
∴α+β=4.
故答案为:4.

∵log2α=4-α,2β=4-β.
而y=log2x(x>0)与y=2x互为反函数,直线y=4-x与直线y=x互相垂直,
∴点P与Q关于直线y=x对称.
∴α=2β=4-β.
∴α+β=4.
故答案为:4.
点评:本题考查了同底的指数函数与对数函数互为反函数的性质、相互垂直的直线之间的关系,属于难题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目