题目内容
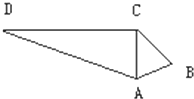 如图在四边形ABCD中,AC⊥DC,△ADC的面积为30cm2,DC=12cm,AB=3cm,BC=4cm求△ABC的面积.
如图在四边形ABCD中,AC⊥DC,△ADC的面积为30cm2,DC=12cm,AB=3cm,BC=4cm求△ABC的面积.考点:余弦定理
专题:解三角形
分析:先由面积公式求得AC=5,再利用勾股定理的逆定理,得到△ABC是直角三角形,即可得到面积.
解答:
解:∵S△ADC=
DC•AC,∴30=
×12×AC,解得AC=5.
在△ABC中,AB2+BC2=32+42=52=AC2,
∴AB⊥BC.
∴S△ABC=
AB•BC=
×3×4=6cm2.
| 1 |
| 2 |
| 1 |
| 2 |
在△ABC中,AB2+BC2=32+42=52=AC2,
∴AB⊥BC.
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了直角三角形的面积计算公式、勾股定理的逆定理,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在△ABC中,AB=
,AC=1,∠A=30°,则△ABC面积为( )
| 3 |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
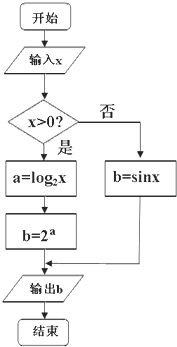 如图所示的程序框图,若两次输入的x值分别是3π和-
如图所示的程序框图,若两次输入的x值分别是3π和-| π |
| 3 |
A、1,
| ||||
B、0,
| ||||
C、-π,-
| ||||
D、3π,-
|
甲船在A处观察到乙船在它的北偏东60°的方向,两船相距a海里,乙船正在向北行驶,若甲船的速度是乙船的
倍,甲船为了尽快追上乙船,应取北偏东θ方向前进,则θ=( )
| 3 |
| A、15° | B、30° |
| C、45° | D、60° |
一个物体的运动方程为s=-
t3+2t2-5,其中s的单位是米,t的单位是秒,那么物体在3秒末的瞬时速度是( )
| 1 |
| 3 |
| A、3米/秒 | B、6米/秒 |
| C、5米/秒 | D、4米/秒 |
在等差数列{an}中,已知a1+a2=4,a2+a3=8,则a7等于( )
| A、7 | B、10 | C、13 | D、19 |