题目内容
已知数列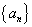 ,首项a 1 =3且2a n+1="S" n?S n-1 (n≥2).
,首项a 1 =3且2a n+1="S" n?S n-1 (n≥2).
(1)求证:{ }是等差数列,并求公差;
}是等差数列,并求公差;
(2)求{a n }的通项公式;
(3)数列{an }中是否存在自然数k0,使得当自然数k≥k 0时使不等式a k>a k+1对任意大于等于k的自然数都成立,若存在求出最小的k值,否则请说明理由.
(1)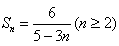
(2)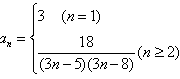
(3)3
解析试题分析:解:⑴由已知当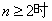
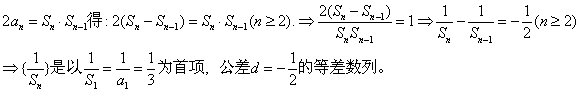 ⑵
⑵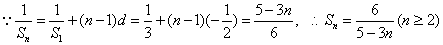
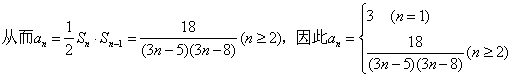
⑶
考点:数列的求和和通项公式的求解
点评:解决的关键是通过数列的递推关系来分析得到证明等差数列,同事借助于关系式得到{a n },然后借助于不等式来得到参数的范围,属于基础题。

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
 满足
满足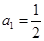 ,
,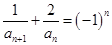
 .
.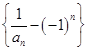
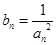
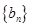 的前
的前 项和
项和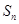 ;
;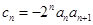 ,数列
,数列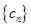 的前
的前 ,求证:
,求证: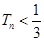 (其中
(其中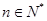 ).
).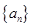 满足:
满足: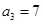 ,
,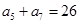 ,
,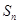 .
.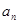 及
及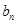 =
=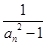 (
(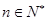 ),求数列
),求数列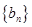 的前
的前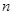 项和
项和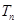 .
.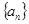 满足:
满足: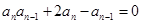 ,
, 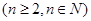 ,
, ,前
,前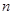 项和为
项和为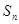 的数列
的数列 满足:
满足: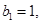
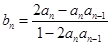
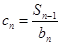
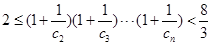
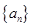 对任意
对任意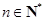 ,满足
,满足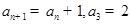 .
.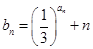 ,求
,求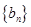 的通项公式及前
的通项公式及前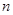 项和.
项和.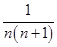 .
.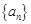 的前
的前 项和为
项和为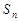 ,若对任意
,若对任意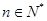 ,都有
,都有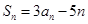 .
.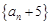 是等比数列,并求数列
是等比数列,并求数列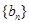 满足
满足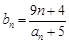 ,问是否存在
,问是否存在 ,使得
,使得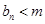 恒成立?如果存在,求出
恒成立?如果存在,求出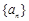 的前n项和为
的前n项和为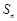 ,点
,点 均在直线
均在直线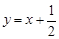 上.
上. 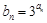 ,试证明数列
,试证明数列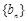 为等比数列.
为等比数列.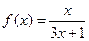 ,数列
,数列 满足
满足
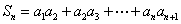 ,求
,求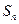 .
.