题目内容
设数列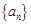 的前
的前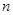 项和为
项和为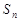 ,若对任意
,若对任意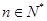 ,都有
,都有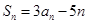 .
.
⑴求数列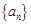 的首项;
的首项;
⑵求证:数列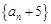 是等比数列,并求数列
是等比数列,并求数列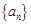 的通项公式;
的通项公式;
⑶数列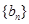 满足
满足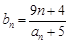 ,问是否存在
,问是否存在 ,使得
,使得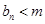 恒成立?如果存在,求出
恒成立?如果存在,求出 的值,如果不存在,说明理由.
的值,如果不存在,说明理由.
⑴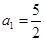 ;⑵
;⑵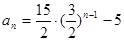 ;⑶
;⑶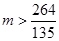 。
。
解析试题分析:⑴∵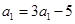 ∴
∴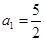 3分
3分
⑵∵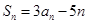 ∴
∴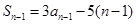 (
(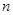 ≥2)
≥2)
∴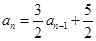 5分
5分
∴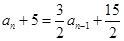

∴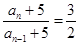 (为常数) (
(为常数) (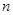 ≥2)
≥2)
∴数列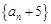 是以
是以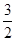 为公比的等比数列 7分
为公比的等比数列 7分
∴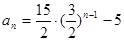 10分
10分
⑶∵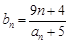 ∴
∴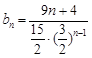
∴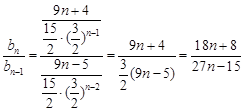 12分
12分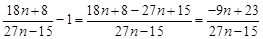 14分
14分
∴当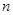 ≥3时,
≥3时,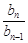 <1; 当
<1; 当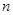 =2时,
=2时,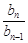 >1
>1
∴当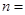 2时,
2时,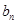 有最大值
有最大值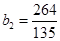
∴ 15分
15分
∴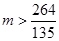 16分
16分
考点:本题主要考查等差数列、等比数列的的基础知识,函数的单调性。
点评:中档题,本题具有较强的综合性,本解答根据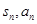 的关系确定通项公式,认识到数列的特征。对于存在性问题,往往先假设存在,本题通过考察
的关系确定通项公式,认识到数列的特征。对于存在性问题,往往先假设存在,本题通过考察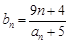 的单调性,利用“放缩法”,证明假设的合理性。
的单调性,利用“放缩法”,证明假设的合理性。

练习册系列答案
相关题目
已知数列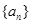 中的
中的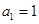 ,且
,且 (
(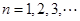 ),则数列
),则数列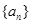 中的
中的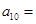 ( )
( )
A.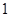 | B. | C.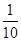 | D.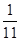 |
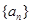 满足
满足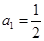 ,
,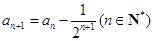 .
.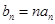 ,数列{bn}的前n项和为Tn,试比较Tn与
,数列{bn}的前n项和为Tn,试比较Tn与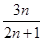 的大小,并予以证明.
的大小,并予以证明.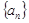 满足
满足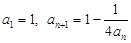 ,其中
,其中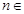 N*.
N*.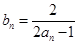 ,求证:数列
,求证:数列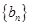 是等差数列,并求出
是等差数列,并求出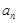 ;
; ,数列
,数列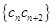 的前
的前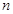 项和为
项和为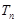 ,是否存在正整数
,是否存在正整数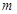 ,使得
,使得 对于
对于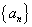 ,首项a 1 =3且2a n+1="S" n?S n-1 (n≥2).
,首项a 1 =3且2a n+1="S" n?S n-1 (n≥2).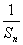 }是等差数列,并求公差;
}是等差数列,并求公差;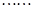
 行里的最后一个数字是多少?
行里的最后一个数字是多少?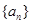 满足:
满足: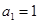 ,
,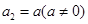 ,
,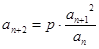 (其中
(其中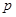 为非零常数,
为非零常数,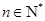 ).
).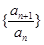 是不是等比数列?
是不是等比数列?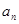 ;
;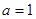 时,令
时,令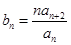 ,
,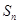 为数列
为数列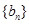 的前
的前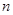 项和,求
项和,求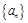 中的各项均为正数,且满足
中的各项均为正数,且满足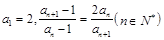 .记
.记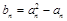 ,数列
,数列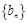 的前
的前 项和为
项和为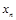 ,且
,且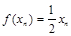 .
. 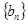 是等比数列;
是等比数列;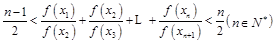 .
.