Question

16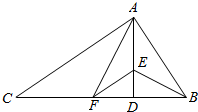．如图，AD是Rt△ABC斜边上的高，BE平分∠ABC交AD于点E，AF平分∠CAD交CD于点F．求证：
（1）EF∥AC；
（2）BF²=BD•BC．

Answer 1

分析 （1）根据角平分线定理，可得$\frac{AE}{ED}$=$\frac{AB}{BD}$，$\frac{CF}{DF}$=$\frac{AC}{AD}$，由△ACD∽△BAD，可得$\frac{AB}{BD}$=$\frac{AC}{AD}$，进而得到答案；
（2）结合（1）中性质，易得△ABF为以B为顶角的等腰三角形，结合射影定理，可得答案．

解答 证明：（1）∵BE平分∠ABC交AD于点E，AF平分∠CAD交CD于点F．
∴$\frac{AE}{ED}$=$\frac{AB}{BD}$，$\frac{CF}{DF}$=$\frac{AC}{AD}$，
∵AD是Rt△ABC斜边上的高，
故△ACD∽△BAD，
则$\frac{AB}{BD}$=$\frac{AC}{AD}$，
即$\frac{AE}{ED}$=$\frac{CF}{DF}$，
即EF∥AC；
（2）由（1）得：
∠EFB=∠C=∠BAD，
∠EFA=∠FAC=∠FAD，
∴∠EFB+∠EFA=∠BAD+∠FAC，
即∠BFA=∠FAB，
即BF=AB，
由射影定理得：AB²=BD•BC．
∴BF²=BD•BC．

点评 本题考查的知识点是相似三角形的判定与性质，角平分线定理，射影定理，难度中档．