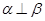题目内容
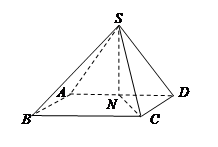
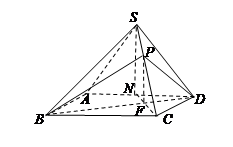
如图,在四棱锥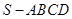 中,底面
中,底面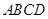 是矩形,
是矩形,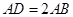 ,
,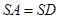 ,
,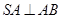 ,
, 是棱
是棱 的中点.
的中点.
(1)求证: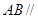 平面
平面 ;
;
(2)求证: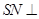 平面
平面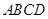 ;
;
(3)在棱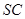 上是否存在一点
上是否存在一点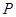 ,使得平面
,使得平面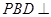 平面
平面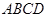 ?若存在,求出
?若存在,求出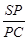 的值;若不存在,说明理由.
的值;若不存在,说明理由.
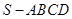 中,底面
中,底面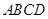 是矩形,
是矩形,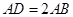 ,
,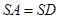 ,
,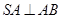 ,
,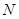 是棱
是棱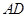 的中点.
的中点.
(1)求证:
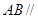 平面
平面 ;
;(2)求证:
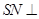 平面
平面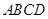 ;
;(3)在棱
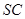 上是否存在一点
上是否存在一点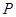 ,使得平面
,使得平面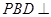 平面
平面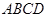 ?若存在,求出
?若存在,求出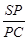 的值;若不存在,说明理由.
的值;若不存在,说明理由.(1)详见解析;(2)详见解析;(3)存在,且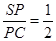 .
.
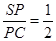 .
.试题分析:(1)先由底面
 为矩形得到
为矩形得到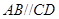 ,然后利用直线与平面平行的判定定理即可证明
,然后利用直线与平面平行的判定定理即可证明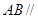 平面
平面 ;(2)先证
;(2)先证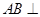 平面
平面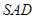 ,于是得到
,于是得到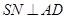 ,然后再利用三线合一得到
,然后再利用三线合一得到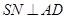 ,然后利用直线与平面垂直的判定定理即可得到
,然后利用直线与平面垂直的判定定理即可得到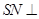 平面
平面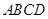 ;(3)利用(2)中的结论
;(3)利用(2)中的结论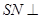 平面
平面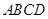 ,结合条件平面
,结合条件平面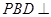 平面
平面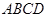 ,得到
,得到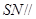 平面
平面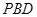 ,连接
,连接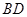 交
交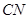 于点
于点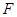 ,利用直线与平面平行的性质定理得到
,利用直线与平面平行的性质定理得到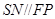 ,最后利用相似三角形来求
,最后利用相似三角形来求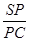 的值.
的值.试题解析:(1)因为底面
 是矩形,
是矩形,所以
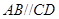 ,
,又因为
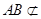 平面
平面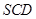 ,
,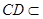 平面
平面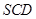 ,
,所以
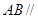 平面
平面 ;
;(2)因为
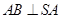 ,
,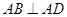 ,
,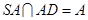 ,
,所以
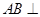 平面
平面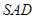 ,
,又因为
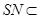 平面
平面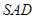 ,
,所以
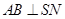 .
.因为
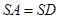 ,且
,且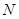 为
为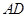 中点,
中点,所以
 .
.又因为
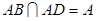 ,
,所以
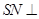 平面
平面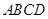 .
.(3)如图,连接
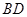 交
交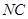 于点
于点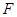 ,在平面
,在平面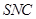 中过
中过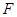 作
作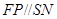 交
交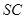 于点
于点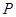 ,连接
,连接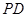 、
、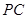 .
.
因为
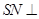 平面
平面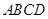 ,
,所以
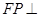 平面
平面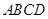 .
.又因为
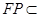 平面
平面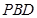 ,
,所以平面
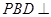 平面
平面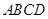 .
.在矩形
 中,因为
中,因为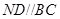 ,
,所以
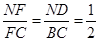 .
.在
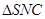 中,因为
中,因为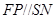 ,
,所以
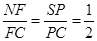 .
.则在棱
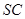 上存在点
上存在点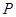 ,使得平面
,使得平面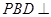 平面
平面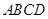 ,此时
,此时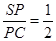 .
.
练习册系列答案
相关题目
 AB.Q是PC上的一点.
AB.Q是PC上的一点.
 中,
中, ,
,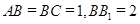 ,求:
,求:
 与
与 所成角的余弦值;
所成角的余弦值;  的距离.
的距离.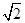 ,PB=2,E、F分别是BC、PC的中点.证明:AD⊥平面DEF.
,PB=2,E、F分别是BC、PC的中点.证明:AD⊥平面DEF.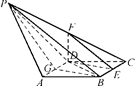
 是两条不重合的直线,
是两条不重合的直线, 是三个不重合的平面,则
是三个不重合的平面,则 的一个充分条件是( )
的一个充分条件是( )



 、
、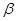 ,直线
,直线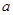 、
、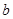 ,
,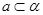 ,
,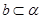 ,则“
,则“ ,
,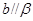 ”是“
”是“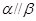 ”的( )
”的( )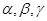 是三个不重合的平面,
是三个不重合的平面, 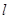 是直线,给出下列四个命题:①若
是直线,给出下列四个命题:①若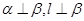 则
则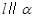 ;②若
;②若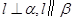 则
则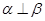 ;③若
;③若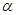 的距离相等,则
的距离相等,则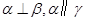 ,则
,则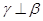 其中正确命题的序号 ( )
其中正确命题的序号 ( )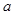 ,b,c是空间三条不同的直线,
,b,c是空间三条不同的直线,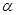 ,
,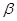 是空间两个不同的平面,则下列命题不成立的是( )
是空间两个不同的平面,则下列命题不成立的是( )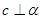 时,若
时,若 ⊥
⊥ ,且
,且