题目内容

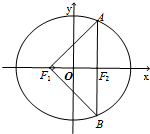
如图，F1、F2是椭圆C1：
x2
a2
+
y2
b2
=1(a＞b＞0)的两焦点，过点F2作AB⊥x轴交椭圆于A、B两点，若△F1AB为等腰直角三角形，且∠AF1B=90°，则椭圆的离心率是（　　）
A．
2
-1		B．
2
2
C．3-2
2
D．2-
2

∵AF2⊥x轴，∴A(c，
b2
a
)．
∵△F1AB为等腰直角三角形，∴|F1F2|=|AF2|，
∴2c=
b2
a
，∴2ac=b2=a2-c2，
∴2e=1-e2，
化为e2+2e-1=0，（e＞0）．
解得e=
-2+2
2
2
=
2
-1．
故选：A．
练习册系列答案
相关题目
若椭圆
x2
16
+
y2
25
=1上一点P到焦点F1的距离为6，则点P到另一个焦点F2的距离为（　　）
A．2B．4C．6D．8
已知椭圆的两个焦点分别为F1（0，-8），F2（0，8），且椭圆上一点到两个焦点的距离之和为20，则此椭圆的方程为______．
命题P“曲线sinα•x2+cosα•y2=1为焦点在y轴上的椭圆”，写出让命题P成立的一个充分条件______（请填写关于α的值或区间）
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的短轴长为4，F1F2分别是椭圆C的左，右焦点，直线y=x与椭圆C在第一象限内的交点为A，△AF1F2的面积为2
6
，点P（x0，y0），是椭圆C上的动点w．
（1）求椭圆C的方程；
（2）若∠F1PF2为钝角，求点P的横坐标x0的取值范围；
（3）求
3
PF1+
2
PA的最小值．
在平面直角坐标系中，已知一个椭圆的中心在原点，左焦点为F(-
3
，0)，且过D（2，0）．
（1）求该椭圆的标准方程；
（2）若P是椭圆上的动点，点A（1，0），求线段PA中点M的轨迹方程．
AB是椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的任意一条与x轴不垂直的弦，O是椭圆的中心，e为椭圆的离心率，M为AB的中点，则KAB•KOM的值为（　　）
A．e-1B．1-eC．e2-1D．1-e2
设P为椭圆
x2
16
+
y2
9
=1上的一点，F1、F2是椭圆的焦点，若|PF1|：|PF2|=3：1，则∠F1PF2的大小为（　　）
A．30°B．60°C．90°D．120°
已知椭圆
x2
a2
+
y2
b2
=1（a＞b＞0），A（2，0）为长轴的一个端点，弦BC过椭圆的中心O，且
AC
•
BC
=0，|
OC
-
OB
|=2|
BC
-
BA
|，则其焦距为（　　）
A．
2
6
3
B．
4
3
3
C．
4
6
3
D．
2
3
3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网