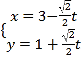题目内容
【题目】已知曲线C的参数方程为![]() (
(![]() 为参数),P是曲线C上的点且对应的参数为
为参数),P是曲线C上的点且对应的参数为![]() ,
,![]() .直线l过点P且倾斜角为
.直线l过点P且倾斜角为![]() .
.
(1)求曲线C的普通方程和直线l的参数方程.
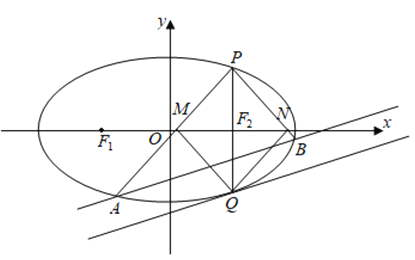
(2)已知直线l与x轴,y轴分别交于![]() ,求证:
,求证:![]() 为定值.
为定值.
【答案】(1)![]() ;
;![]() (t为参数)(2)证明见解析
(t为参数)(2)证明见解析
【解析】
(1)由曲线C的参数方程为![]() ,利用
,利用![]() 消去参数
消去参数![]() 可得曲线C的普通方程, 由直线l过点
可得曲线C的普通方程, 由直线l过点![]() 且倾斜角为
且倾斜角为![]() ,所以直线l的参数方程为
,所以直线l的参数方程为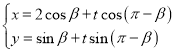 ,化简可得答案.
,化简可得答案.
(2)由![]() ,所以
,所以![]() ,由直线l与x轴,y轴分别交于
,由直线l与x轴,y轴分别交于![]() ,可得A对应的参数
,可得A对应的参数![]() , B对应的参数
, B对应的参数![]() 的值,计算可得
的值,计算可得![]() 为定值.
为定值.
(1)解:曲线C的普通方程为![]() ,
,
因为直线l过点![]() 且倾斜角为
且倾斜角为![]() ,
,
所以直线l的参数方程为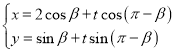 ,
,
即![]() (t为参数).
(t为参数).
(2)证明:因为![]() ,所以
,所以![]() ,
,
所以由![]() ,得A对应的参数
,得A对应的参数![]() ,
,
由![]() ,得B对应的参数
,得B对应的参数![]() ,
,
所以![]() 为定值.
为定值.

 备战中考寒假系列答案
备战中考寒假系列答案【题目】某学校为了解高一新生的体能情况,在入学后不久,组织了一次体能测试,按成绩分为优秀、良好、一般、较差四个档次.现随机抽取120名学生的成绩,其条形图如下:
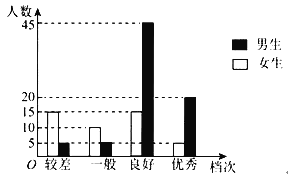
(1)将优秀、良好、一般归为合格,较差归为不合格,试根据条形图完成下面的2×2列联表,并判断能否在犯错误的概率不超过0.01的前提下认为学生的成绩与性别有关.
合格 | 不合格 | 合计 | |
男生 | |||
女生 | |||
合计 |
(2)学校为了解学生以前参加课外活动的情况,利用分层抽样的方法从120名学生中抽取24名学生参加一个座谈会.
①座谈会上抽取2名学生汇报以前参加课外活动的情况,求恰好抽到测试成绩一个优秀与一个较差的学生的概率;
②为全面提高学生的体能,学校专门安排专职教师对全校测试成绩较差的学生在课外活动时进行专项训练,通过一段时间的训陈后,测试合格率达到了![]() .若某班有4名学生参加这个专项训陈,求训练后测试合格人数ξ的分布列与数学期望.
.若某班有4名学生参加这个专项训陈,求训练后测试合格人数ξ的分布列与数学期望.
附:K2![]() ,其中n=a+b+c+d
,其中n=a+b+c+d
P(K2≥k0) | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |