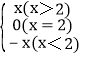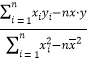Question

【题目】[选项4-4：坐标系与参数方程]
在直角坐标系xOy中，圆C的方程为（x+6）2+y2=25．
（1）以坐标原点为极点，x轴正半轴为极轴建立极坐标系，求C的极坐标方程；
（2）直线l的参数方程是 （t为参数），l与C交与A，B两点，|AB|= ，求l的斜率．

Answer 1

【答案】
（1）

解：∵圆C的方程为（x+6）2+y2=25，

∴x2+y2+12x+11=0，

∵ρ2=x2+y2，x=ρcosα，y=ρsinα，

∴C的极坐标方程为ρ2+12ρcosα+11=0

（2）

∵直线l的参数方程是 （t为参数），

∴直线l的一般方程y=tanαx，

∵l与C交与A，B两点，|AB|= ，圆C的圆心C（﹣6，0），半径r=5，

∴圆心C（﹣6，0）到直线距离d= = ，

解得tan2α= ，∴tanα=± =± ．

∴l的斜率k=±

【解析】（1）把圆C的标准方程化为一般方程，由此利用ρ2=x2+y2 ， x=ρcosα，y=ρsinα，能求出圆C的极坐标方程．（2）由直线l的参数方程求出直线l的一般方程，再求出圆心到直线距离，由此能求出直线l的斜率．；本题考查圆的极坐标方程的求法，考查直线的斜率的求法，是中档题，解题时要认真审题，注意点到直线公式、圆的性质的合理运用．
【考点精析】本题主要考查了圆的标准方程的相关知识点，需要掌握圆的标准方程：；圆心为A(a,b),半径为r的圆的方程才能正确解答此题．