题目内容
【题目】甲乙两人进行某种游戏比赛,规定:每一次胜者得1分,负者得0分;当其中一人的得分比另一人的得分多2分时即赢得这场游戏,比赛随之结束.同时规定:比赛次数最多不超过20次,即经20次比赛,得分多者赢得这场游戏,得分相等为和局.已知每次比赛甲获胜的概率为可![]() ,乙获胜的概率为
,乙获胜的概率为![]() .假定各次比赛的结果是相互独立的,比赛经
.假定各次比赛的结果是相互独立的,比赛经![]() 次结束.求
次结束.求![]() 的期望
的期望![]() 的变化范围.
的变化范围.
【答案】见解析
【解析】
记比赛经![]() 次结束的概率为
次结束的概率为![]() .
.
若![]() 为奇数,则甲乙得分之差亦为奇数,比赛无法结束.
为奇数,则甲乙得分之差亦为奇数,比赛无法结束.
考虑![]() 为偶数时,头两次比赛的结果:1.甲连胜或乙连胜两次,称为有胜负的两次,此结果出现的概率为
为偶数时,头两次比赛的结果:1.甲连胜或乙连胜两次,称为有胜负的两次,此结果出现的概率为![]() ; 2.甲乙各胜一次,称为无胜负的两次,此结果有两种情形,故出现的概率为
; 2.甲乙各胜一次,称为无胜负的两次,此结果有两种情形,故出现的概率为![]() .于是,1、2两次,3、4两次,
.于是,1、2两次,3、4两次,![]() ,
,![]() 、
、![]() 两次均未分胜负.若
两次均未分胜负.若![]() ,则第
,则第![]() 、
、![]() 两次为有胜负的两次.从而,
两次为有胜负的两次.从而,![]() .
.
若![]() ,则比赛必须结束.从而,
,则比赛必须结束.从而,![]() .
.
综上,![]() .令
.令![]() .则
.则
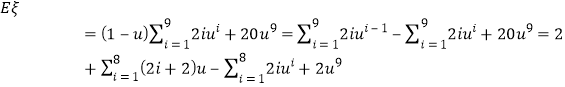
![]() .因此
.因此![]() ,所以
,所以![]() .
.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
【题目】为调研高中生的作文水平.在某市普通高中的某次联考中,参考的文科生与理科生人数之比为![]() ,且成绩分布在
,且成绩分布在![]() 的范围内,规定分数在50以上(含50)的作文被评为“优秀作文”,按文理科用分层抽样的方法抽取400人的成绩作为样本,得到成绩的频率分布直方图,如图所示.其中
的范围内,规定分数在50以上(含50)的作文被评为“优秀作文”,按文理科用分层抽样的方法抽取400人的成绩作为样本,得到成绩的频率分布直方图,如图所示.其中![]() 构成以2为公比的等比数列.
构成以2为公比的等比数列.
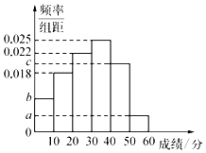
(1)求![]() 的值;
的值;
(2)填写下面![]() 列联表,能否在犯错误的概率不超过0.01的情况下认为“获得优秀作文”与“学生的文理科”有关?
列联表,能否在犯错误的概率不超过0.01的情况下认为“获得优秀作文”与“学生的文理科”有关?
文科生 | 理科生 | 合计 | |
获奖 | 6 | ||
不获奖 | |||
合计 | 400 |
(3)将上述调查所得的频率视为概率,现从全市参考学生中,任意抽取2名学生,记“获得优秀作文”的学生人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附: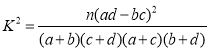 ,其中
,其中![]() .
.
| .15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |


