题目内容
如图,P是双曲线
-
=1(a>0,b>0,xy≠0)上的动点,F1、F2是双曲线的焦点,M是∠F1PF2的平分线上一点,且
•
=0.某同学用以下方法研究|OM|:延长F2M交PF1于点N,可知△PNF2为等腰三角形,且M为F2M的中点,得|OM|=
|NF1|=…=a.类似地:P是椭圆
+
=1(a>b>0,xy≠0)上的动点,F1、F2是椭圆的焦点,M是∠F1PF2的平分线上一点,且
•
=0.则|OM|的取值范围是 ______.

| x2 |
| a2 |
| y2 |
| b2 |
| F2M |
| MP |
| 1 |
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
| F2M |
| MP |

延长F2M交PF1于点N,可知△PNF2为等腰三角形,
且M为F2M的中点,
则|OM|=
|NF1|=a-|F2M|
∵a-c<|F2M|<a
故0<|OM|<c=
故|OM|的取值范围是(0,
)
故答案为:(0,
)
且M为F2M的中点,
则|OM|=
| 1 |
| 2 |
∵a-c<|F2M|<a
故0<|OM|<c=
| a2-b2 |
故|OM|的取值范围是(0,
| a2-b2 |
故答案为:(0,
| a2-b2 |

练习册系列答案
相关题目
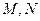 是椭圆
是椭圆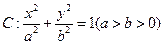 上关于原点
上关于原点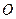 对称的两个点,点
对称的两个点,点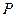 是椭圆
是椭圆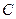 上任意一点,且直线
上任意一点,且直线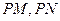 的斜率都存在(记为
的斜率都存在(记为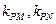 ),则
),则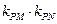 是与点
是与点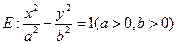 的类似性质,并加以证明。
的类似性质,并加以证明。