题目内容
已知椭圆具有性质:若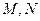 是椭圆
是椭圆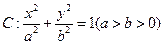 上关于原点
上关于原点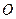 对称的两个点,点
对称的两个点,点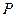 是椭圆
是椭圆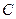 上任意一点,且直线
上任意一点,且直线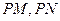 的斜率都存在(记为
的斜率都存在(记为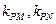 ),则
),则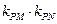 是与点
是与点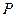 位置无关的定值。试写出双曲线
位置无关的定值。试写出双曲线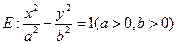 的类似性质,并加以证明。
的类似性质,并加以证明。
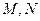 是椭圆
是椭圆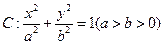 上关于原点
上关于原点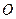 对称的两个点,点
对称的两个点,点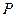 是椭圆
是椭圆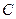 上任意一点,且直线
上任意一点,且直线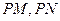 的斜率都存在(记为
的斜率都存在(记为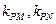 ),则
),则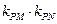 是与点
是与点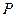 位置无关的定值。试写出双曲线
位置无关的定值。试写出双曲线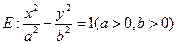 的类似性质,并加以证明。
的类似性质,并加以证明。双曲线的类似性质为:若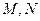 是双曲线
是双曲线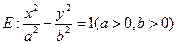 上关于原点
上关于原点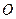 对称的两个点,点
对称的两个点,点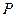 是双曲线
是双曲线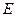 上任意一点,且直线
上任意一点,且直线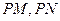 的斜率都存在(记为
的斜率都存在(记为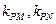 ),则
),则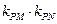 是与点
是与点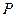 位置无关的定值。证明见解析。
位置无关的定值。证明见解析。
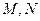 是双曲线
是双曲线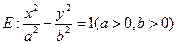 上关于原点
上关于原点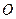 对称的两个点,点
对称的两个点,点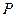 是双曲线
是双曲线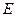 上任意一点,且直线
上任意一点,且直线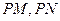 的斜率都存在(记为
的斜率都存在(记为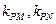 ),则
),则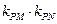 是与点
是与点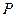 位置无关的定值。证明见解析。
位置无关的定值。证明见解析。双曲线的类似性质为:若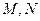 是双曲线
是双曲线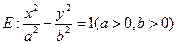 上关于原点
上关于原点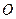 对称的两个点,点
对称的两个点,点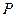 是双曲线
是双曲线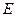 上任意一点,且直线
上任意一点,且直线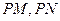 的斜率都存在(记为
的斜率都存在(记为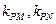 ),则
),则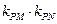 是与点
是与点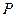 位置无关的定值。
位置无关的定值。
证明如下:
设点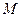 的坐标为
的坐标为 ,则点
,则点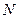 的坐标为
的坐标为 ,且
,且 ,
,
又设点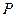 的坐标为
的坐标为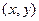 ,则
,则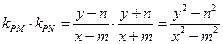 。
。
将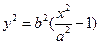 和
和 代入上式,得
代入上式,得 (定值)。
(定值)。
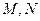 是双曲线
是双曲线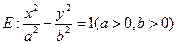 上关于原点
上关于原点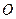 对称的两个点,点
对称的两个点,点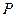 是双曲线
是双曲线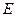 上任意一点,且直线
上任意一点,且直线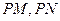 的斜率都存在(记为
的斜率都存在(记为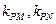 ),则
),则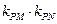 是与点
是与点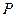 位置无关的定值。
位置无关的定值。证明如下:
设点
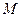 的坐标为
的坐标为 ,则点
,则点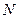 的坐标为
的坐标为 ,且
,且 ,
,又设点
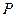 的坐标为
的坐标为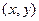 ,则
,则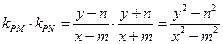 。
。将
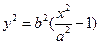 和
和 代入上式,得
代入上式,得 (定值)。
(定值)。
练习册系列答案
相关题目
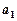 ,
,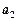
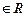 ,
,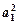
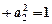 ,则
,则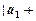
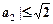 .”可以如下证明:构造函数
.”可以如下证明:构造函数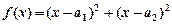 ,则
,则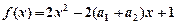 ,因为对一切
,因为对一切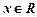 ,恒有
,恒有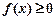 ,所以
,所以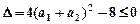 ,故得
,故得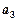
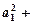
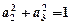 ,求证
,求证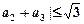 ;
; 边形
边形 中的每条边和每条对角线都被染为n种颜色中的一种颜色.问:对怎样的n,存在一种染色方式,使得对于这n种颜色中的任何3种不同颜色,都能找到一个三角形,其顶点为多边形
中的每条边和每条对角线都被染为n种颜色中的一种颜色.问:对怎样的n,存在一种染色方式,使得对于这n种颜色中的任何3种不同颜色,都能找到一个三角形,其顶点为多边形
 出发依次沿图中线段到达
出发依次沿图中线段到达 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 各点,最后又回到
各点,最后又回到 ,
, ,
,
 .欲知此质点所走路程,至少需要测量
.欲知此质点所走路程,至少需要测量 条线段的长度,
条线段的长度, ( )
( )




 ,分别以
,分别以 三边为轴将三角形旋转一周所得旋转体的体积记为
三边为轴将三角形旋转一周所得旋转体的体积记为 ,请比较
,请比较