题目内容
已知一个四面体其中五条棱的长分别为1,1,1,1, ,则此四面体体积的最大值是
,则此四面体体积的最大值是
A. | B. | C.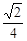 | D. |
A
解析试题分析:设四面体为P-ABC,则设PC=X,AB= ,其余的各边为1,那么取AB的中点D,那么连接PD,因此可知,AB垂直与平面PCD,则棱锥的体积可以运用以PCD为底面,高为AD,BD的两个三棱锥体积的和来表示,因此只要求解底面积的最大值即可。由于PD=CD=
,其余的各边为1,那么取AB的中点D,那么连接PD,因此可知,AB垂直与平面PCD,则棱锥的体积可以运用以PCD为底面,高为AD,BD的两个三棱锥体积的和来表示,因此只要求解底面积的最大值即可。由于PD=CD=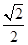 ,那么可知三角形PDC的面积越大,体积越大,因此可知面积的最大值为
,那么可知三角形PDC的面积越大,体积越大,因此可知面积的最大值为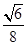 ,也就是当PD垂直于CD时,面积最大,因此可四面体的体积的最大值为
,也就是当PD垂直于CD时,面积最大,因此可四面体的体积的最大值为 ,选A.
,选A.
考点:考查了多面体体积的运用。
点评:解决该试题的关键是对于四面体的边长的合理布置,然后进行作相应的辅助线,来借助于垂直的性质,表示多面体的体积,进而得到表达式,结合函数来求解最值,属于中档题。

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
若一个棱锥的三视图如图所示,则它的体积为( )
A. | B. | C.1 | D. |
在正三棱柱 中,若AB=2,
中,若AB=2,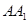 =1,则点A到平面
=1,则点A到平面 的距离为( )
的距离为( )
A. | B.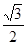 | C. | D. |
一个棱锥的三视图如图,则该棱锥的体积是
A. | B. |
C. | D. |
某几何体的三视图如图所示,则该几何体的体积为( )
A. | B. |
C. | D. |
右图是一个几何体的正视图和侧视图。其俯视图是面积为 的矩形。则该几何体的表面积是
的矩形。则该几何体的表面积是
| A.8 | B. |
| C.16 | D. |
从点 出发的三条射线
出发的三条射线 两两成
两两成 角,且分别与球
角,且分别与球 相切于
相切于 三点,若球的体积为
三点,若球的体积为 ,则
,则 两点之间的距离为( )
两点之间的距离为( )
A. | B. | C.1.5 | D.2 |
 和直线
和直线 ,
, 所围成的平面图形,绕
所围成的平面图形,绕 轴旋转一周所得到的旋转体为
轴旋转一周所得到的旋转体为 ;由同时满足
;由同时满足 ,
, ,
, ,
, 的点
的点 构成的平面图形,绕
构成的平面图形,绕 .根据祖暅原理等知识,通过考察
.根据祖暅原理等知识,通过考察



 的侧棱与底面边长都相等,
的侧棱与底面边长都相等, 在底面
在底面 内的射影为
内的射影为
 与底面
与底面


