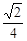题目内容
已知三棱柱 的侧棱与底面边长都相等,
的侧棱与底面边长都相等, 在底面
在底面 内的射影为
内的射影为
 的中心,则
的中心,则 与底面
与底面 所成角的正弦值等于( )
所成角的正弦值等于( )
A. | B. | C. | D. |
B
解析试题分析:根据题意可知,ABC的中心为O,连CO并延长交AB于D,过B1作B1E⊥AB交AB的延长线于E,再过B1作B1F⊥平面ABC交平面ABC于F。
设AB=a。∵AB=AC=BC=a,O是△ABC的中心,∴CD⊥AD、AD=BD=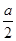 ,∴CD=
,∴CD=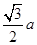
显然有: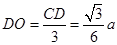 。
。
∵O是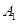 在平面ABC上的射影,∴
在平面ABC上的射影,∴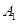 O⊥平面ABC,∴AD⊥
O⊥平面ABC,∴AD⊥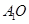 ,又AD⊥CD、CD∩
,又AD⊥CD、CD∩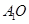 =O,∴AD⊥平面
=O,∴AD⊥平面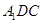 ,∴AD⊥
,∴AD⊥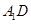 。
。
由 =a、AD=
=a、AD=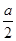 、
、 ⊥
⊥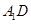 ,得:
,得: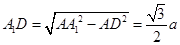 。∵
。∵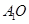 ⊥平面ABC,∴
⊥平面ABC,∴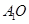 ⊥
⊥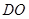
由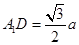 、
、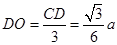 、
、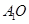 ⊥
⊥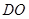 ,得:
,得: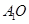 =
=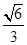
∵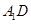 ⊥
⊥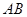 、
、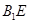 ⊥
⊥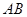 ,∴
,∴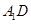 ∥
∥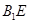
∵ 是三棱柱,∴
是三棱柱,∴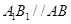 。
。
由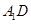 ∥
∥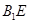 ,
,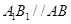 得:
得: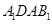 是平行四边形,∴
是平行四边形,∴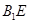 =
=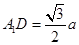 、
、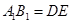 =a显然,有:AE=AD+DE=
=a显然,有:AE=AD+DE=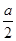 +a=
+a=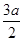 。
。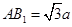
∵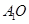 ⊥平面ABC,
⊥平面ABC,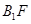 ⊥平面ABC,∴
⊥平面ABC,∴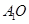 ∥
∥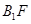 ,∴
,∴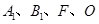 共面。
共面。
∵ 是三棱柱,∴
是三棱柱,∴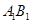 ∥平面ABC,而平面ABC∩平面
∥平面ABC,而平面ABC∩平面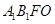 =OF,∴
=OF,∴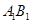 ∥OF。由
∥OF。由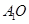 ∥
∥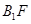 、
、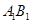 ∥OF,得:
∥OF,得: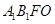 是平行四边形,∴
是平行四边形,∴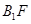 =
=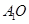 =
=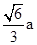
∵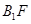 ⊥平面ABC,∴
⊥平面ABC,∴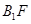 ⊥AF。,得:sin∠
⊥AF。,得:sin∠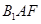 =
=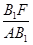 =
=
考点:本试题考查了线面角的求解知识。
点评:对于该试题中的线面角的求解,关键是建立线面垂直的背景,同时根据已知的边长和侧棱长的关系式得到角度,进而求解运算,属于难度试题。

 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案设 是三个不重合的平面,l是直线,给出下列命题:
是三个不重合的平面,l是直线,给出下列命题:
①若 ,则
,则 ; ②若
; ②若
③若l上存在两点到 的距离相等,则
的距离相等,则 ; ④若
; ④若
其中正确的命题是( )
| A.①② | B.②③ | C.②④ | D.③④ |
图是一个几何体的三视图,根据图中数据,可得该几何体的表面积、体积分别是
A.32 、 、 | B.16 、 、 |
C.12 、 、 | D.8 、 、 |
利用斜二测画法可以得到:
①三角形的直观图是三角形;②平行四边形的直观图是平行四边形;
③正方形的直观图是正方形;④菱形的直观图是菱形. 以上结论正确的是( )
| A.①② | B.① | C.③④ | D.①②③④ |
某几何体的三视图如图所示,则它的体积是( )
A.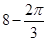 | B. |
C. | D. |
过空间任意一点引三条不共面的直线,它们所确定的平面个数是( )
| A.1 | B.2 | C.3 | D.1或3 |
若一个球的表面积为4 ,则这个球的体积是( )
,则这个球的体积是( )
A. | B. | C. | D. |
 ,则此四面体体积的最大值是
,则此四面体体积的最大值是