题目内容
已知圆O:x2+y2=4,AB为圆O的任意一条直径,P(1,3),Q(-1,0),则当PA+AB+BQ最小时,直径AB所在的直线方程为______.
∵已知圆O:x2+y2=4,AB为圆O的任意一条直径,P(1,3),Q(-1,0),
设点R(1,0)、点A(x,y),
则点B(-x,-y),PA+AB+BQ=
+4+
=
+
+4=PA+AR+4.
由于
表示圆上的点A(x,y)到点P(1,3)的距离,
而
表示圆上的点A(x,y)到点R(1,0)的距离,
故当点A是PR与圆的交点时,PA+AR=
+
最小,
即PA+AB+BQ最小,此时,点A(1,
),故AB的斜率为
=
,
故直线AB的方程为 y=
x,
故答案为 y=
x.
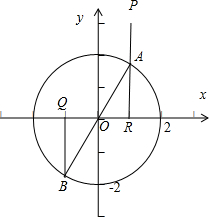
设点R(1,0)、点A(x,y),
则点B(-x,-y),PA+AB+BQ=
| (x-1)2+(y-3)2 |
| (-x+1)2+y2 |
=
| (x-1)2+(y-3)2 |
| (x-1)2+y2 |
由于
| (x-1)2+(y-3)2 |
而
| (x-1)2+y2 |
故当点A是PR与圆的交点时,PA+AR=
| (x-1)2+(y-3)2 |
| (x-1)2+y2 |
即PA+AB+BQ最小,此时,点A(1,
| 3 |
| ||
| 1-0 |
| 3 |
故直线AB的方程为 y=
| 3 |
故答案为 y=
| 3 |


练习册系列答案
相关题目
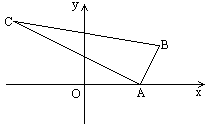
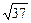 ,求直线l的方程.
,求直线l的方程.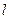 过点P(2,3),并与
过点P(2,3),并与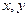 轴正半轴交于A,B二点。
轴正半轴交于A,B二点。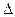 AOB面积为
AOB面积为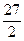 时,求直线
时,求直线