题目内容
已知直线l的斜率为6,且被两坐标轴所截得的线段长为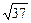 ,求直线l的方程.
,求直线l的方程.
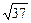 ,求直线l的方程.
,求直线l的方程.y=6x±6.
设所求直线l的方程为y=kx+b.
∵k=6,∴方程为y=6x+b.
令x=0,∴y=b,与y轴的交点为(0,b);
令y=0,∴x=-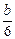 ,与x轴的交点为(-
,与x轴的交点为(-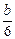 ,0).
,0).
根据勾股定理得(-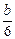 )2+b2=37,
)2+b2=37,
∴b=±6.因此直线l的方程为y=6x±6.°.
∵k=6,∴方程为y=6x+b.
令x=0,∴y=b,与y轴的交点为(0,b);
令y=0,∴x=-
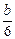 ,与x轴的交点为(-
,与x轴的交点为(-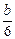 ,0).
,0).根据勾股定理得(-
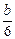 )2+b2=37,
)2+b2=37,∴b=±6.因此直线l的方程为y=6x±6.°.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
 ,则直线
,则直线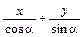 =1必不经过
=1必不经过 ( )
( )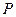 到点
到点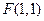 和直线
和直线 的距离相等,则点
的距离相等,则点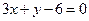
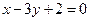
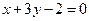
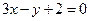
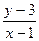 =2,x、y∈R},B={(x,y)|4x+ay=16,x、y∈R},若A∩B=
=2,x、y∈R},B={(x,y)|4x+ay=16,x、y∈R},若A∩B=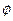 ,则实数a的值为 .
,则实数a的值为 .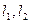 的倾斜角分别是
的倾斜角分别是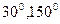 ,点A在
,点A在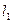 上,点B在
上,点B在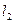 上,且
上,且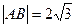 ,(1)若P为线段AB的中点,求点P的轨迹方程(2)若P为线段AB的中点, 定点
,(1)若P为线段AB的中点,求点P的轨迹方程(2)若P为线段AB的中点, 定点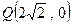 ,且
,且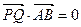 ,求点P
,求点P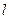 过原点且平分
过原点且平分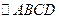 的面积,若平行四边形的两个顶点为
的面积,若平行四边形的两个顶点为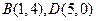 ,则直线
,则直线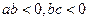 ,则直线
,则直线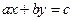 通过( )
通过( )