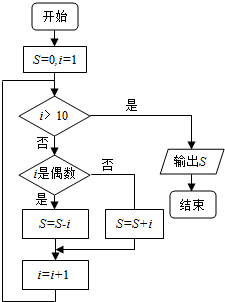
题目内容
12.一倒置圆锥体的母线长为10cm,底面半径为6cm,(1)求圆锥体的高;
(2)一球刚好放进该圆锥体中,求这个球的半径以及此时圆锥体剩余的空间.
分析 (1)根据圆锥的定义,利用勾股定理加以计算,可得圆锥的高等于8cm;
(2)作出圆锥的轴截面如图,根据球与侧面、底面相切,利用相似三角形的性质列式列式,算出内切球的半径R,进而利用球的体积公式可算出答案.
解答 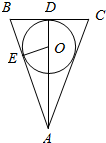 解:(1)设圆锥的底面半径为r,高为h,母线长为l,
解:(1)设圆锥的底面半径为r,高为h,母线长为l,
∵l=10cm,r=6cm,
∴h=$\sqrt{{l}^{2}-{r}^{2}}$=$\sqrt{100-36}$=8cm
即圆锥的高等于8cm;
(2)作出圆锥的轴截面如图,球于圆锥侧面相切,
则OE⊥AB于E,BD⊥AD于D,OE=OD=R,(R为球的半径)
则△AEO∽△ADB,可得OE:BD=AO:AB,
即$\frac{R}{6}=\frac{8-R}{10}$,
解之得球半径R=3cm,
因此球的体积V=$\frac{4}{3}{πR}^{3}$=36πcm3.
圆锥的体积V=$\frac{1}{3}{πr}^{2}h$=96πcm3.
故圆锥体剩余的空间体积为60πcm3.
点评 本题给出圆锥满足的条件,求它的高并求内切球的体积.着重考查了圆锥的定义、球的体积公式、相似三角形的判定与性质等知识,属于中档题.

练习册系列答案
相关题目
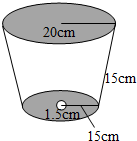 如图所示,一个圆台形花盆盆口半径为20cm,盆底半径为15cm,底部渗水圆孔半径为1.5cm,盆壁长15cm,那么花盆的表面积约为多少平方厘米(π取3.14,结果精确到1cm2)
如图所示,一个圆台形花盆盆口半径为20cm,盆底半径为15cm,底部渗水圆孔半径为1.5cm,盆壁长15cm,那么花盆的表面积约为多少平方厘米(π取3.14,结果精确到1cm2)