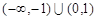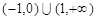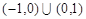题目内容
对于 上可导的任意函数
上可导的任意函数 ,若满足
,若满足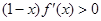 ,则必有 ( )
,则必有 ( )
A.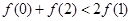 | B.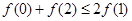 |
C.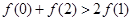 | D.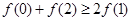 |
A
解析试题分析:
解:∵(x-1)f'(x)<0,∴x>1时,f′(x)<0;x<1时,f′(x)>0,∴f(x)在(1,+∝)为减函数;在(-∝,1)上为则增函数,∴f(2)<f(1), f(0)<f(1),∴f(0)+f(2)<2f(1).,故选A
考点:函数的单调性
点评:利用导函数的符号能判断函数的单调性,当导函数大于0则函数递增;当导函数小于0则函数单调递减.

练习册系列答案
相关题目
设函数 及其导函数
及其导函数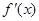 都是定义在R上的函数,则“
都是定义在R上的函数,则“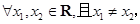
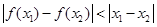 ”是“
”是“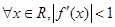 ”的
”的
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
“函数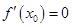 ”是“可导函数
”是“可导函数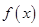 在点
在点 处取到极值”的 条件。 ( )
处取到极值”的 条件。 ( )
| A.充分不必要 | B.必要不充分 | C.充要 | D.既不充分也不必要 |
曲线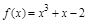 上点
上点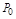 处的切线垂直于直线
处的切线垂直于直线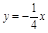 ,则点P0的坐标是( )
,则点P0的坐标是( )
A.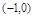 | B.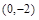 | C.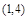 | D.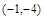 或 或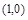 |
曲线 在
在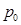 处的切线平行于直线
处的切线平行于直线 ,则
,则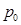 点的坐标为( )
点的坐标为( )
A.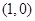 | B.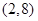 |
C.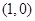 和 和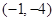 | D.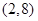 和 和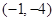 |
已知函数f(x)=x2+2x+blnx,若函数f(x)在(0,1)上单调,则实数b的取值范围是
| A.b≥ 0 | B.b<-4 | C.b≥0或b≤-4 | D.b>0或b<-4 |
设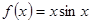 ,
,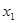 、
、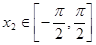 ,且
,且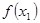 >
>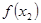 ,则下列结论必成立的是( )
,则下列结论必成立的是( )
A.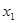 > >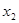 | B.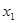 + +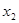 >0 >0 | C.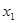 < <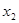 | D.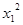 > > |
 具有下列特征:
具有下列特征: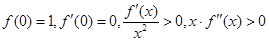 ,则
,则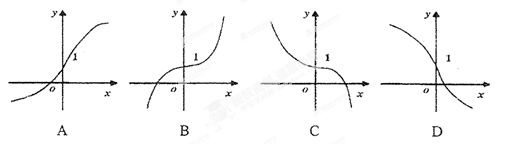
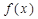 是定义在R上的奇函数,且
是定义在R上的奇函数,且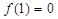 ,当
,当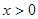 时,有
时,有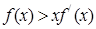 恒成立,则不等式
恒成立,则不等式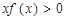 的解集为( )
的解集为( )