题目内容
设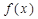 是定义在R上的奇函数,且
是定义在R上的奇函数,且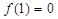 ,当
,当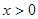 时,有
时,有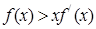 恒成立,则不等式
恒成立,则不等式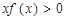 的解集为( )
的解集为( )
A. | B.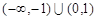 |
C.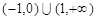 | D.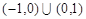 |
D
解析试题分析:不等式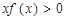 的解集等价于不等式
的解集等价于不等式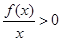 的解集。令
的解集。令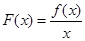 ,由于当
,由于当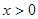 时,有
时,有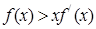 恒成立,则
恒成立,则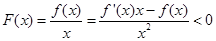 ,所以函数
,所以函数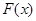 在
在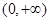 上是减函数,又
上是减函数,又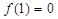 ,则
,则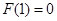 ,又由于
,又由于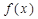 是定义在R上的奇函数,即有
是定义在R上的奇函数,即有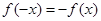 ,则函数
,则函数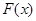 满足
满足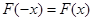 ,是偶函数。画出函数
,是偶函数。画出函数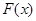 的图像如下,则不等式
的图像如下,则不等式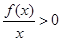 的解集为
的解集为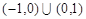 。故选D。
。故选D。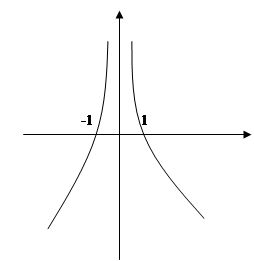
考点:不等式的解集
点评:求不是具体不等式的解集,常通过画出函数的图像,然后从图像得到不等式的解集。

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
已知函数f(x)=2-|x|,则 =
=
| A.3 | B.4 | C.3.5 | D.4.5 |
已知函数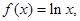 ,
, 直线与函数
直线与函数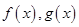 的图象都相切,且与
的图象都相切,且与 图象的切点为(1,f(x)),则
图象的切点为(1,f(x)),则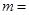 ( )
( )
A. | B. | C. | D. |
对于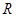 上可导的任意函数
上可导的任意函数 ,若满足
,若满足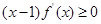 ,则必有( )
,则必有( )
A.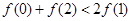 | B.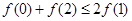 |
C.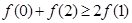 | D.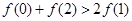 |
对于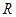 上可导的任意函数
上可导的任意函数 ,若满足
,若满足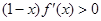 ,则必有 ( )
,则必有 ( )
A.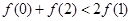 | B.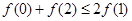 |
C.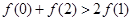 | D.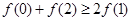 |
已知 ,
,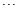
 则
则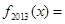 ( )
( )
A. | B.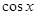 | C. | D.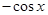 |
若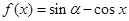 ,则
,则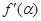 等于( )
等于( )
A.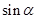 | B.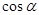 | C.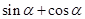 | D.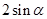 |
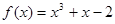 的一条切线平行于直线
的一条切线平行于直线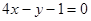 ,则除切点外切线与曲线的另一交点坐标可以是( )
,则除切点外切线与曲线的另一交点坐标可以是( )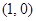
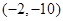
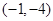
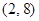
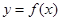 的导函数在区间
的导函数在区间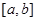 上是增函数,则函数
上是增函数,则函数