题目内容
设函数 及其导函数
及其导函数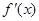 都是定义在R上的函数,则“
都是定义在R上的函数,则“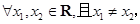
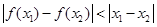 ”是“
”是“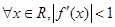 ”的
”的
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
B
解析试题分析:根据题意,由于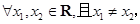
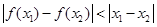 ”则说明函数在定义域内递增函数,且在任意两点的斜率的绝对值小于1,那么结论是“
”则说明函数在定义域内递增函数,且在任意两点的斜率的绝对值小于1,那么结论是“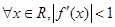 ”表示的为任意点处的切线的斜率的绝对值小于1, 则可知条件不可推出结论,反之能成立,故为必要而不充分条件,选B.
”表示的为任意点处的切线的斜率的绝对值小于1, 则可知条件不可推出结论,反之能成立,故为必要而不充分条件,选B.
考点:导数的运用
点评:主要是考查了导数来判定函数单调性的运用,属于基础题。

练习册系列答案
相关题目
若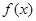 的定义域为
的定义域为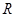 ,
,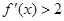 恒成立,
恒成立,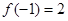 ,则
,则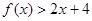 解集为( )
解集为( )
A.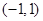 | B.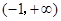 | C.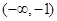 | D.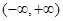 |
下列式子不正确的是
A.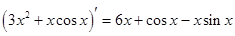 | B.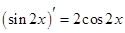 |
C.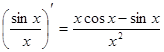 | D.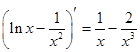 |
已知函数f(x)=2-|x|,则 =
=
| A.3 | B.4 | C.3.5 | D.4.5 |
已知函数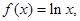 ,
, 直线与函数
直线与函数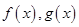 的图象都相切,且与
的图象都相切,且与 图象的切点为(1,f(x)),则
图象的切点为(1,f(x)),则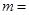 ( )
( )
A. | B. | C. | D. |
对于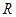 上可导的任意函数
上可导的任意函数 ,若满足
,若满足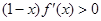 ,则必有 ( )
,则必有 ( )
A.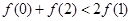 | B.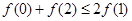 |
C.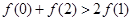 | D.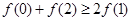 |
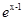 +1图像上的动点,O为坐标原点,当1PQ1最小时,直线OQ交函数y=
+1图像上的动点,O为坐标原点,当1PQ1最小时,直线OQ交函数y=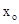 ,
,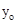 )(异于Q点),则
)(异于Q点),则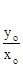 =
=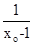
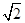
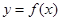 的导函数在区间
的导函数在区间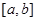 上是增函数,则函数
上是增函数,则函数

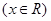 满足
满足 ,则当
,则当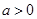 时,
时, 和
和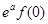 的大小关系为( )
的大小关系为( )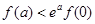 (B)
(B)
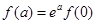 (C)
(C)