题目内容
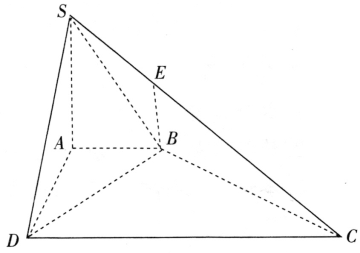
【题目】如图,已知正方体![]() ,
,![]() 为棱
为棱![]() 的中点,
的中点,![]() 为棱
为棱![]() 的动点,设直线
的动点,设直线![]() 为平面
为平面![]() 与平面
与平面![]() 的交线,直线
的交线,直线![]() 为平面
为平面![]() 与平面
与平面![]() 的交线,下列结论中错误的是( )
的交线,下列结论中错误的是( )

A.![]() 平面
平面![]() B.平面
B.平面![]() 与平面
与平面![]() 不垂直
不垂直
C.平面![]() 与平面
与平面![]() 可能平行D.直线
可能平行D.直线![]() 与直线
与直线![]() 可能不平行
可能不平行
【答案】D
【解析】
在正方体![]() 中,可得
中,可得![]() ,根据线面平行的判定定理和性质定理可得
,根据线面平行的判定定理和性质定理可得![]() ,可判断选项A结论;分别取
,可判断选项A结论;分别取![]() 中点
中点![]() ,连
,连![]() ,则
,则![]() 为平面
为平面![]() 与平面
与平面![]() 的平面角,判断
的平面角,判断![]() 是否为直角,即可判断选项B的结论;若
是否为直角,即可判断选项B的结论;若![]() 为
为![]() 中点时,可证平面
中点时,可证平面![]() 与平面
与平面![]() 平行,即可判断选项C的结论;根据面面平行的性质定理可得
平行,即可判断选项C的结论;根据面面平行的性质定理可得![]() ,即可判断选项D的结论.
,即可判断选项D的结论.
在正方体![]() 中,四边形
中,四边形![]() 为矩形,
为矩形,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
平面![]() 与平面
与平面![]() ,
,
选项A,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,选项A结论正确;
,选项A结论正确;
选项B,分别取![]() 中点
中点![]() ,连
,连![]() ,
,
设正方体的边长为![]() ,设
,设![]() ,
,
则![]() ,
,
![]() ,同理
,同理![]() ,
,
![]() 为平面
为平面![]() 与平面
与平面![]() 的平面角,
的平面角,
在![]() 中,
中,![]() ,
,
![]() ,
,![]() 不是直角,
不是直角,
所以平面![]() 与平面
与平面![]() 不垂直,选项B结论正确;
不垂直,选项B结论正确;
选项C,若![]() 为
为![]() 中点,取
中点,取![]() 中点
中点![]() 连
连![]() ,
,
则![]() ,又
,又![]() 为棱
为棱![]() 的中点,
的中点,
![]() ,四边形
,四边形![]() 为平行四边形,
为平行四边形,
![]() 面
面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,同理
,同理![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
![]() 平面
平面![]() 平面
平面![]() ,选项C结论正确;
,选项C结论正确;
选项D,在正方体中,平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]()
![]() ,选项D结论不正确.
,选项D结论不正确.
故选:D.


练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
【题目】为调查某社区居民的业余生活状况,研究这一社区居民在20:00-22:00时间段的休闲方式与性别的关系,随机调查了该社区80人,得到下面的数据表:
休闲方式 性别 | 看电视 | 看书 | 合计 |
男 | 10 | 50 | 60 |
女 | 10 | 10 | 20 |
合计 | 20 | 60 | 80 |
(1)根据以上数据,能否有![]() 的把握认为“在20:00-22:00时间段的休闲方式与性别有关系”?
的把握认为“在20:00-22:00时间段的休闲方式与性别有关系”?
(2)将此样本的频率估计为总体的概率,随机调查3名在该社区的男性,设调查的3人在这一时间段以看书为休闲方式的人数为随机变量![]() ,求
,求![]() 的数学期望和方差.
的数学期望和方差.
参考公式与数据![]() 对应
对应![]() ,
,![]() 对应
对应![]() .
.