ÌâÄżÄÚÈĘ
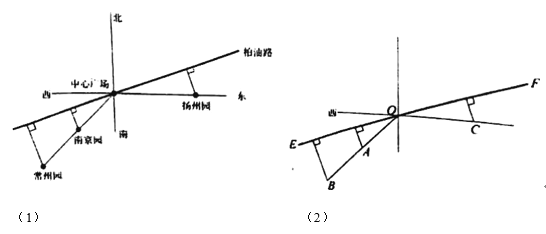
ĄŸÌâÄżĄżœËŐÊĄÔ°Č©»áÓĐÒ»ÖĐĐÄč㳥ŁŹÄÏŸ©Ô°ŁŹłŁÖĘÔ°¶ŒÔÚÖĐĐÄč㳥”ÄÄÏÆ«Îś45Ąă·œÏòÉÏŁŹ”œÖĐĐÄč㳥”ÄŸàÀë·Ö±đÎȘ![]() kmŁŹ
kmŁŹ![]() kmŁ»ŃïÖĘÔ°ÔÚÖĐĐÄč㳥”ÄŐ궫·œÏòŁŹ”œÖĐĐÄč㳥”ÄŸàÀëÎȘ
kmŁ»ŃïÖĘÔ°ÔÚÖĐĐÄč㳥”ÄŐ궫·œÏòŁŹ”œÖĐĐÄč㳥”ÄŸàÀëÎȘ![]() kmŁźčæ»źœšÉèÒ»Ìő±ÊÖ±”Ä°ŰÓÍ·Ž©čęÖĐĐÄč㳥ŁŹÇÒœ«ÄÏŸ©Ô°ŁŹłŁÖĘÔ°ŁŹŃïÖĘÔ°”œ°ŰÓÍ·”ÄŚî¶Ì·Ÿ¶ÆÌÉèłÉ¶ìÂŃÊŻÂ·ŁšÈçÍŒ(1)Ąą(2)Ł©ŁźÒŃÖȘÆÌÉèĂż¶Î¶ìÂŃÊŻÂ·”Ä·ŃÓĂŁšÍòÔȘŁ©ÓëÆ䳀¶È”ÄÆœ·œłÉŐę±ÈŁŹ±ÈÀęÏ”ÊęÎȘ2ŁźÉè°ŰÓÍ·ÓëŐ궫·œÏò”ÄŒĐœÇŁŹŒŽÍŒ(2)ÖĐĄÏCOFÎȘ
kmŁźčæ»źœšÉèÒ»Ìő±ÊÖ±”Ä°ŰÓÍ·Ž©čęÖĐĐÄč㳥ŁŹÇÒœ«ÄÏŸ©Ô°ŁŹłŁÖĘÔ°ŁŹŃïÖĘÔ°”œ°ŰÓÍ·”ÄŚî¶Ì·Ÿ¶ÆÌÉèłÉ¶ìÂŃÊŻÂ·ŁšÈçÍŒ(1)Ąą(2)Ł©ŁźÒŃÖȘÆÌÉèĂż¶Î¶ìÂŃÊŻÂ·”Ä·ŃÓĂŁšÍòÔȘŁ©ÓëÆ䳀¶È”ÄÆœ·œłÉŐę±ÈŁŹ±ÈÀęÏ”ÊęÎȘ2ŁźÉè°ŰÓÍ·ÓëŐ궫·œÏò”ÄŒĐœÇŁŹŒŽÍŒ(2)ÖĐĄÏCOFÎȘ![]() Łš
Łš![]() (0ŁŹ
(0ŁŹ![]() )Ł©ŁŹÆÌÉèÈę¶Î¶ìÂŃÊŻÂ·”ÄŚÜ·ŃÓĂÎȘyŁšÍòÔȘŁ©Łź
)Ł©ŁŹÆÌÉèÈę¶Î¶ìÂŃÊŻÂ·”ÄŚÜ·ŃÓĂÎȘyŁšÍòÔȘŁ©Łź
Łš1Ł©ÇóÄÏŸ©Ô°”œ°ŰÓÍ·”ÄŚî¶ÌŸàÀë![]() čŰÓÚ
čŰÓÚ![]() ”ıíŽïÊœŁ»
”ıíŽïÊœŁ»
Łš2Ł©Çóy”ÄŚîĐĄÖ”Œ°ŽËʱtan![]() ”ÄÖ”Łź
”ÄÖ”Łź
ĄŸŽđ°žĄżŁš1Ł©![]() Ł»Łš2Ł©ÆÌÉèÈęÌő¶ìÂŃÊŻÂ·”ÄŚÜ·ŃÓĂÎȘ(
Ł»Łš2Ł©ÆÌÉèÈęÌő¶ìÂŃÊŻÂ·”ÄŚÜ·ŃÓĂÎȘ(![]() )ÍòÔȘŁŹŽËʱ
)ÍòÔȘŁŹŽËʱ![]() ”ÄÖ”ÎȘ
”ÄÖ”ÎȘ![]() .
.
ĄŸœâÎöĄż
Łš1Ł©ÓÉĄÏCOF=ŠÈŁŹÄÏŸ©Ô°ÔÚÖĐĐÄč㳥”ÄÄÏÆ«Îś45Ąă·œÏòÉÏŁŹÇÒ”œÖĐĐÄč㳥”ÄŸàÀëÎȘ![]() ŁŹÇółöĄÏAOE=
ŁŹÇółöĄÏAOE=![]() ŁŹÓÉŽËÄÜÇółöÄÏŸ©Ô°”œ°ŰÓÍ·”ÄŚî¶ÌŸàÀëd1čŰÓڊȔıíŽïÊœŁź
ŁŹÓÉŽËÄÜÇółöÄÏŸ©Ô°”œ°ŰÓÍ·”ÄŚî¶ÌŸàÀëd1čŰÓڊȔıíŽïÊœŁź
Łš2Ł©·Ö±đÉè”ăBŁŹC”œÖ±ÏßEF”ÄŸàÀëÎȘd2ŁŹd3ŁŹÔò![]() ŁŹÇółöy=2[Łš
ŁŹÇółöy=2[Łš![]() Ł©2+Łš2
Ł©2+Łš2![]() Ł©2+Łš
Ł©2+Łš![]() Ł©2]=20©10
Ł©2]=20©10![]() sinŁš2
sinŁš2![]() Ł©ŁŹŠÈĄÊŁš0ŁŹ
Ł©ŁŹŠÈĄÊŁš0ŁŹ![]() Ł©ŁŹÓÉŽËÄÜÇółöÆÌÉèÈęÌő¶ìÂŃÊŻÂ·”ÄŚÜ·ŃÓĂy”ÄŚîĐĄÖ”Œ°ŽËʱtanŠÈ”ÄÖ”Łź
Ł©ŁŹÓÉŽËÄÜÇółöÆÌÉèÈęÌő¶ìÂŃÊŻÂ·”ÄŚÜ·ŃÓĂy”ÄŚîĐĄÖ”Œ°ŽËʱtanŠÈ”ÄÖ”Łź
Łš1Ł©ĄßĄÏCOF=ŠÈŁŹ
ÄÏŸ©Ô°ÔÚÖĐĐÄč㳥”ÄÄÏÆ«Îś45Ąă·œÏòÉÏŁŹÇÒ”œÖĐĐÄč㳥”ÄŸàÀëÎȘ![]()
ĄàĄÏAOE=![]() ŁŹ
ŁŹ
ĄàÄÏŸ©Ô°”œ°ŰÓÍ·”ÄŚî¶ÌŸàÀëd1čŰÓڊȔıíŽïÊœÎȘd1=![]() sinŁš
sinŁš![]() ©ŠÈŁ©Łź
©ŠÈŁ©Łź
Łš2Ł©·Ö±đÉè”ăBŁŹC”œÖ±ÏßEF”ÄŸàÀëÎȘd2ŁŹd3Łź
ÓÉŁš1Ł©ÖȘŁș![]() ŁŹ
ŁŹ
Ąày=2[Łš![]() Ł©2+Łš2
Ł©2+Łš2![]() Ł©2+Łš
Ł©2+Łš![]() Ł©2]
Ł©2]
=20[![]() +
+![]() ]
]
=20©10Łšsin2ŠÈ+cos2ŠÈŁ©
=20©10![]() sinŁš2
sinŁš2![]() Ł©ŁŹŠÈĄÊŁš0ŁŹ
Ł©ŁŹŠÈĄÊŁš0ŁŹ![]() Ł©ŁŹ
Ł©ŁŹ
Ąß![]() Ąà
Ąà![]() ŁŹ
ŁŹ
Ąà”±2![]() =
=![]() ʱŁŹymin=20©10
ʱŁŹymin=20©10![]() ŁšÍòÔȘŁ©
ŁšÍòÔȘŁ©
ŽËʱ2![]() ŁŹ
ŁŹ
Ąàtan2ŠÈ=![]() =1ŁŹ
=1ŁŹ
œâ”ĂŁștan![]() ŁŹ
ŁŹ
ĄàÆÌÉèÈęÌő¶ìÂŃÊŻÂ·”ÄŚÜ·ŃÓĂÎȘŁš20©10![]() Ł©ÍòÔȘŁŹŽËʱtanŠÈ”ÄÖ”ÎȘ
Ł©ÍòÔȘŁŹŽËʱtanŠÈ”ÄÖ”ÎȘ![]() Łź
Łź

ĄŸÌâÄżĄżÍłŒÆѧÖĐŁŹŸłŁÓĂ»·±ÈĄąÍŹ±ÈÀŽœűĐĐÊęŸĘ±ÈœÏŁŹ»·±ÈÊÇÖž±ŸÆÚÍłŒÆÊęŸĘÓëÉÏÆÚ±ÈœÏŁŹÈç![]() Äê
Äê![]() ÔÂÓë
ÔÂÓë![]() Äê
Äê![]() ÔÂÏà±ÈŁŹÍŹ±ÈÊÇÖž±ŸÆÚÊęŸĘÓëÀúÊ·ÍŹÊ±ÆÚ±ÈœÏŁŹÈç
ÔÂÏà±ÈŁŹÍŹ±ÈÊÇÖž±ŸÆÚÊęŸĘÓëÀúÊ·ÍŹÊ±ÆÚ±ÈœÏŁŹÈç![]() Äê
Äê![]() ÔÂÓë
ÔÂÓë![]() Äê
Äê![]() ÔÂÏà±È.
ÔÂÏà±È.
»·±ÈÔöł€ÂÊ![]() Łš±ŸÆÚÊę
Łš±ŸÆÚÊę![]() ÉÏÆÚÊ꣩
ÉÏÆÚÊ꣩![]() ÉÏÆÚÊę
ÉÏÆÚÊę![]() ŁŹ
ŁŹ
ÍŹ±ÈÔöł€ÂÊ![]() Łš±ŸÆÚÊę
Łš±ŸÆÚÊę![]() ÍŹÆÚÊ꣩
ÍŹÆÚÊ꣩![]() ÍŹÆÚÊę
ÍŹÆÚÊę![]() .
.
ϱíÊÇÄł”ŰÇűœü![]() žöÔÂÀŽ”ÄÏû·ŃŐßĐĆĐÄÖžÊę”ÄÍłŒÆÊęŸĘŁș
žöÔÂÀŽ”ÄÏû·ŃŐßĐĆĐÄÖžÊę”ÄÍłŒÆÊęŸĘŁș
ĐòșĆ |
|
|
|
|
|
|
|
|
ʱŒä |
|
|
|
|
|
|
|
|
Ïû·ŃŐßĐĆĐÄÖžÊę |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2017Äê
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]()
![]() ÇóžĂ”ŰÇű
ÇóžĂ”ŰÇű![]() Äê
Äê![]() ÔÂÏû·ŃŐßĐĆĐÄÖžÊę”ÄÍŹ±ÈÔöł€ÂÊŁš°Ù·Ö±ÈĐÎʜϱŁÁôŐûÊ꣩Ł»
ÔÂÏû·ŃŐßĐĆĐÄÖžÊę”ÄÍŹ±ÈÔöł€ÂÊŁš°Ù·Ö±ÈĐÎʜϱŁÁôŐûÊ꣩Ł»
![]() łę
łę![]() Äê
Äê![]() ÔÂÒÔÍ⣏žĂ”ŰÇűÏû·ŃŐßĐĆĐÄÖžÊęÔ»·±ÈÔöł€ÂÊÎȘžșÊę”ÄÓĐŒžžöÔÂŁż
ÔÂÒÔÍ⣏žĂ”ŰÇűÏû·ŃŐßĐĆĐÄÖžÊęÔ»·±ÈÔöł€ÂÊÎȘžșÊę”ÄÓĐŒžžöÔÂŁż
![]() ÓÉÒÔÉÏÊęŸĘżÉĆĐ¶ÏŁŹĐòșĆ
ÓÉÒÔÉÏÊęŸĘżÉĆĐ¶ÏŁŹĐòșĆ![]() ÓëžĂ”ŰÇűÏû·ŃŐßĐĆĐÄÖžÊę
ÓëžĂ”ŰÇűÏû·ŃŐßĐĆĐÄÖžÊę![]() ŸßÓĐÏßĐÔÏàčŰčŰÏ”ŁŹĐŽłö
ŸßÓĐÏßĐÔÏàčŰčŰÏ”ŁŹĐŽłö![]() čŰÓÚ
čŰÓÚ![]() ”ÄÏßĐÔ»Űčé·œłÌ
”ÄÏßĐÔ»Űčé·œłÌ![]() Łš
Łš![]() ŁŹ
ŁŹ![]() ±ŁÁô
±ŁÁô![]() λХÊ꣩ŁŹČąÒÀŽËÔ€ČâžĂ”ŰÇű
λХÊ꣩ŁŹČąÒÀŽËÔ€ČâžĂ”ŰÇű![]() Äê
Äê![]() Ô”ÄÏû·ŃŐßĐĆĐÄÖžÊ꣚œáčû±ŁÁô
Ô”ÄÏû·ŃŐßĐĆĐÄÖžÊ꣚œáčû±ŁÁô![]() λХÊ꣏ČÎżŒÊęŸĘÓëč«ÊœŁș
λХÊ꣏ČÎżŒÊęŸĘÓëč«ÊœŁș![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ Ł©
Ł©