题目内容
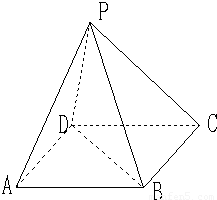
P是平行四边形ABCD外一点,∠DAB=60°,AB=2AD=2a,△PDC是正三角形,BC⊥PD(1)证明:平面PBD⊥平面ABCD;
(2)求二面角P-BC-D的余弦值;
(3)求三棱锥B-ADP的体积.
【答案】分析:(1)依题意,可证AB2=BD2+AD2⇒AD⊥BD,结合已知BC⊥PD可证AD⊥平面PBD,从而可证平面PBD⊥平面ABCD;
(2)可证∠PBD为二面角P-BC-D的平面角,再利用余弦定理计算即可;
(3)通过体积转化公式VB-ADP=VA-PBD及可求得答案.
解答:证明:(1)在△ABD中,∠DAB=60°,AB=2AD=2a,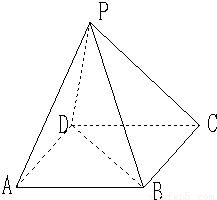
∴由余弦定理得:BD2=AD2+AB2-2AD•ABcos∠DAB=a2+4a2-2×a×2a× =3a2,
=3a2,
∴BD=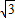 a;
a;
∴AB2=BD2+AD2,
∴△ABD是直角三角形,AD⊥BD,
又BC⊥PD,BC∥AD,
∴AD⊥PD,PD∩BD=D,
∴AD⊥平面PBD,AD?平面ABCD,
∴平面PBD⊥平面ABCD;
(2)由AD⊥平面PBD,BC∥AD知,BC⊥平面PBD,PB?平面PBD,
∴BC⊥PB;①
又∠ADB=∠DBC=90°,
∴DB⊥BC;②
平面PBC∩平面DBC=BC,
∴∠PBD为二面角P-BC-D的平面角.
∵△PDC是边长为2a正三角形,BD=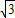 a,
a,
由BC⊥PB知,△PBC为直角三角形,由斜边PC=2a,直角边BC=a可得PB=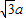 ;
;
∴cos∠PBD=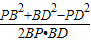 =
=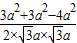 =
= ;
;
(3)∵AD⊥平面PBD,
∴VB-ADP=VA-PBD
= •AD•S△PBD
•AD•S△PBD
= ×a×
×a× PB•BD•sin∠PBD
PB•BD•sin∠PBD
= a•
a•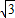 a•
a•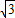 a•
a•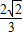
=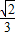 a3.
a3.
点评:本题考查平面与平面垂直的判定,考查二面角的平面角及求法,考查余弦定理与棱锥的体积的综合应用,属于难题.
(2)可证∠PBD为二面角P-BC-D的平面角,再利用余弦定理计算即可;
(3)通过体积转化公式VB-ADP=VA-PBD及可求得答案.
解答:证明:(1)在△ABD中,∠DAB=60°,AB=2AD=2a,

∴由余弦定理得:BD2=AD2+AB2-2AD•ABcos∠DAB=a2+4a2-2×a×2a×
 =3a2,
=3a2,∴BD=
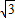 a;
a;∴AB2=BD2+AD2,
∴△ABD是直角三角形,AD⊥BD,
又BC⊥PD,BC∥AD,
∴AD⊥PD,PD∩BD=D,
∴AD⊥平面PBD,AD?平面ABCD,
∴平面PBD⊥平面ABCD;
(2)由AD⊥平面PBD,BC∥AD知,BC⊥平面PBD,PB?平面PBD,
∴BC⊥PB;①
又∠ADB=∠DBC=90°,
∴DB⊥BC;②
平面PBC∩平面DBC=BC,
∴∠PBD为二面角P-BC-D的平面角.
∵△PDC是边长为2a正三角形,BD=
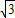 a,
a,由BC⊥PB知,△PBC为直角三角形,由斜边PC=2a,直角边BC=a可得PB=
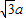 ;
;∴cos∠PBD=
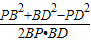 =
=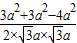 =
= ;
;(3)∵AD⊥平面PBD,
∴VB-ADP=VA-PBD
=
 •AD•S△PBD
•AD•S△PBD=
 ×a×
×a× PB•BD•sin∠PBD
PB•BD•sin∠PBD=
 a•
a•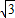 a•
a•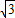 a•
a•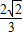
=
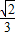 a3.
a3.点评:本题考查平面与平面垂直的判定,考查二面角的平面角及求法,考查余弦定理与棱锥的体积的综合应用,属于难题.

练习册系列答案
相关题目
 在平面直角坐标系xOy中,已知四边形OABC是平行四边形,且点
在平面直角坐标系xOy中,已知四边形OABC是平行四边形,且点 在平面直角坐标系xoy中,已知四边形OABC是平行四边形,A(4,0),C(1,
在平面直角坐标系xoy中,已知四边形OABC是平行四边形,A(4,0),C(1, 如图,四棱锥P-ABCD的底面是平行四边形,PA⊥平面ABCD,AC⊥AB,AB=PA,点E是PD上的点,且DE=λEP(0<λ≤1).
如图,四棱锥P-ABCD的底面是平行四边形,PA⊥平面ABCD,AC⊥AB,AB=PA,点E是PD上的点,且DE=λEP(0<λ≤1). 已知如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABC,垂足G在AD上,且
已知如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABC,垂足G在AD上,且