Question

已知三点A（4，0），B（t，2），C（6，t），t∈R．
（1）若△ABC是直角三角形，求t的值；
（2）O为原点，若四边形OACB是平行四边形，且点P（x，y）在其内部及其边界上，求2y-x的最小值．

Answer 1

分析：（1）先求出

AB

=(t-4，2)，

AC

=(2，t)，

BC

=(6-t，t-2)，再分别讨论A，B，C为直角是对应的t的值即可；
（2）先根据其为平行四边形求出t=2；再结合图象即可得到2y-x的最小值．

解答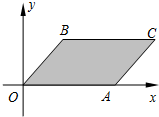：解：（1）由条件，

AB

=(t-4，2)，

AC

=(2，t)，

BC

=(6-t，t-2)，
若直角△ABC中，∠A=90°，则

AB

•

AC

=0，即2（t-4）+2t=0，∴t=2；
若直角△ABC中，∠B=90°，则

AB

•

BC

=0，即（t-4）（6-t）+2（t-2）=0，∴t=6±2

2

；
若直角△ABC中，∠C=90°，则

AC

•

BC

=0，即2（6-t）+t（t-2）=0，无解，
所以，满足条件的t的值为2或6±2

2

．
（2）若四边形OABC是平行四边形，则

OA

=

BC

，
即（4，0）=（6-t，t-2），
∴t=2．
作出平行四边形OABC区域，
设z=2y-x，则y=

1

2

x+

z

2

，
由图知，当点P（x，y）与A（4，0）重合时，z取最小值，且最小值为8．

点评：本题主要考察平面向量的综合问题以及线性规划的应用．是对知识的综合考察，属于中档题目．