题目内容
给出下列四个命题:
①若函数f(x)=a(x3-x)在区间( ,
, )为减函数,则a>0;
)为减函数,则a>0;
②函数f(x)=lg(ax+1)的定义域是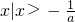 ;
;
③当x>0且x≠1时,有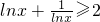 ;
;
④函数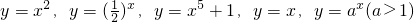 中,幂函数有2个.
中,幂函数有2个.
所有正确命题的个数是
- A.1
- B.2
- C.3
- D.4
B
分析:对于①若函数f(x)=a(x3-x)在区间( ,
, )为减函数,则f′(x)<0在区间(
)为减函数,则f′(x)<0在区间( ,
, )上恒成立,即可求得a的范围;对于②当a>0时,函数f(x)=lg(ax+1)的定义域是
)上恒成立,即可求得a的范围;对于②当a>0时,函数f(x)=lg(ax+1)的定义域是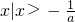 ;对于③当x>0且x≠1时,因lnx不一定大于0,故不一定有
;对于③当x>0且x≠1时,因lnx不一定大于0,故不一定有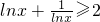 ;对于④函数中,幂函数有y=x2,y=x,共2个.
;对于④函数中,幂函数有y=x2,y=x,共2个.
解答:①若函数f(x)=a(x3-x)在区间( ,
, )为减函数,则f′(x)<0在区间(
)为减函数,则f′(x)<0在区间( ,
, )上恒成立,即:a(3x2-1)<0?a>0;故①正确;
)上恒成立,即:a(3x2-1)<0?a>0;故①正确;
②当a>0时,函数f(x)=lg(ax+1)的定义域是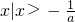 ;故其错;
;故其错;
③当x>0且x≠1时,因lnx不一定大于0,故不一定有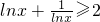 ;故③错;
;故③错;
④函数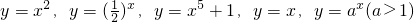 中,幂函数有y=x2,y=x,共2个.故其正确.
中,幂函数有y=x2,y=x,共2个.故其正确.
所有正确命题的个数是2.
故选B.
点评:本小题主要考查函数单调性的应用、函数恒成立问题、不等式的解法等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.
分析:对于①若函数f(x)=a(x3-x)在区间(
 ,
, )为减函数,则f′(x)<0在区间(
)为减函数,则f′(x)<0在区间( ,
, )上恒成立,即可求得a的范围;对于②当a>0时,函数f(x)=lg(ax+1)的定义域是
)上恒成立,即可求得a的范围;对于②当a>0时,函数f(x)=lg(ax+1)的定义域是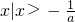 ;对于③当x>0且x≠1时,因lnx不一定大于0,故不一定有
;对于③当x>0且x≠1时,因lnx不一定大于0,故不一定有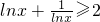 ;对于④函数中,幂函数有y=x2,y=x,共2个.
;对于④函数中,幂函数有y=x2,y=x,共2个.解答:①若函数f(x)=a(x3-x)在区间(
 ,
, )为减函数,则f′(x)<0在区间(
)为减函数,则f′(x)<0在区间( ,
, )上恒成立,即:a(3x2-1)<0?a>0;故①正确;
)上恒成立,即:a(3x2-1)<0?a>0;故①正确;②当a>0时,函数f(x)=lg(ax+1)的定义域是
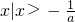 ;故其错;
;故其错;③当x>0且x≠1时,因lnx不一定大于0,故不一定有
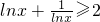 ;故③错;
;故③错;④函数
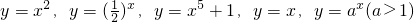 中,幂函数有y=x2,y=x,共2个.故其正确.
中,幂函数有y=x2,y=x,共2个.故其正确.所有正确命题的个数是2.
故选B.
点评:本小题主要考查函数单调性的应用、函数恒成立问题、不等式的解法等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.

练习册系列答案
相关题目