题目内容
【题目】在发生公共卫生事件期间，有专业机构认为该事件在一段时间内没有发生大规模群体感染的标志为“连续
天，每天新增疑似病例不超过
人”．过去日，甲、乙、丙、丁四地新增疑似病例数据信息如下，则一定符合该标志的是（ ）
甲地：总体平均数
，且中位数为
；
乙地：总体平均数为
，且标准差
；
丙地：总体平均数，且极差
；
丁地：众数为
，且极差
．
A.甲地B.乙地C.丙地D.丁地
【答案】CD
【解析】
根据条件，举例说明甲地和乙地，根据极差的概念，说明每天新增疑似病例的最大值，判断丙地和丁地.
甲地：满足总体平均数
，且中位数为
，举例7天的新增疑似病例为0，0，0，0，5，6，7，则不符合该标志；
乙地：若7天新增疑似病例为1，1，1，1，2，2，6，满足平均数为2，标准差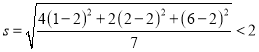
，
但不符合该标志；
丙地：由极差
可知，若新增疑似病例最多超过5人，比如6人，那么最小值不低于4人，
那么总体平均数
就不正确，故每天新增疑似病例低于5人，故丙地符合该标志；
丁地：因为众数为1，且极差
，所以新增疑似病例的最大值
，所以丁地符合该标志.
故选：CD
练习册系列答案
七星图书口算速算天天练系列答案
初中学业考试导与练系列答案
相关题目
【题目】某幼儿园雏鹰班的生活老师统计2018年上半年每个月的20日的昼夜温差
，
和患感冒的小朋友人数（
/人）的数据如下：
温差 |
|
|
|
|
|
|
患感冒人数 | 8 | 11 | 14 | 20 | 23 | 26 |
其中
，
，
.
（Ⅰ）请用相关系数加以说明是否可用线性回归模型拟合与
（Ⅱ）建立关于
的回归方程（精确到
），预测当昼夜温差升高
时患感冒的小朋友的人数会有什么变化？（人数精确到整数）
参考数据：
．参考公式：相关系数：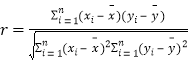
，回归直线方程是
，
,
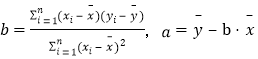