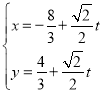题目内容
【题目】十九大提出:坚决打赢脱贫攻坚战,做到精准扶贫.某县积极引导农民种植一种名贵中药材,从而大大提升了该县村民的经济收入.2019年年底,该机构从该县种植的这种名贵药材的农户中随机抽取了100户,统计了他们2019年因种植,中药材所获纯利润(单位:万元)的情况(假定农户因种植中药材这一项一年最多获利11万元),统计结果如下表所示:
![]()
(1)由表可以认为,该县农户种植中药材所获纯利润Z(单位:万元)近似地服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() (每组数据取区间的中点值),
(每组数据取区间的中点值),![]() 近似为样本方差
近似为样本方差![]() .若该县有1万户农户种植了该中药材,试估算所获纯利润Z在区间(1.9,8.2)的户数;
.若该县有1万户农户种植了该中药材,试估算所获纯利润Z在区间(1.9,8.2)的户数;
(2)为答谢广大农户的积极参与,该调查机构针对参与调查的农户举行了抽奖活动,抽奖规则如下:在一箱子中放置5个除颜色外完全相同的小球,其中红球1个,黑球4个.让农户从箱子中随机取出一个小球,若取到红球,则抽奖结束;若取到黑球,则将黑球放回箱中,让他继续取球,直到取到红球为止(取球次数不超过10次).若农户取到红球,则视为中奖,获得2000元的奖励,若一直未取到红球,则视为不中奖.现农户张明参加了抽奖活动,记他中奖时取球的次数为随机变量X,他取球的次数为随机变量Y.
①证明:![]() 为等比数列;
为等比数列;
②求Y的数学期望.(精确到0.001)
参考数据:![]() .若随机变量
.若随机变量![]() 则
则![]()
![]() .
.
【答案】(1)![]() ;(2)①证明见解析;②
;(2)①证明见解析;②![]() ..
..
【解析】
(1)根据题意求出样本平均数![]() 即可得出
即可得出![]() 即
即![]() ,则可根据
,则可根据![]() ,求出其所获纯利润Z在区间(1.9,8.2)的户数;
,求出其所获纯利润Z在区间(1.9,8.2)的户数;
(2) ①因为每次取球都恰有![]() 的概率取到红球,即
的概率取到红球,即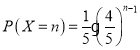 ,则可证明之.
,则可证明之.
②根据①所求的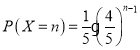 ,根据当
,根据当![]() 时,
时,![]() ,代入
,代入![]() ,再利用错位相减求出其值即可.
,再利用错位相减求出其值即可.
(1)由题意知:

所以样本平均数为![]() (万元),
(万元),
所以![]() ,
,
所以![]() ,
,
而![]() .
.
故1万户农户中,Z落在区间![]() 的户数约为
的户数约为![]() .
.
(2)①每次取球都恰有![]() 的概率取到红球.
的概率取到红球.
则有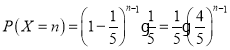 ,
,
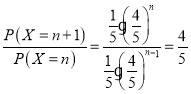 ,
,![]()
故![]() 为以
为以![]() 为首项
为首项![]() 为公比的等比数列.
为公比的等比数列.
②由①可知,当![]() 时,
时,![]() ,
,
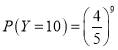 .
.
故Y的数学期望为
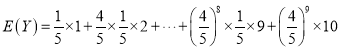
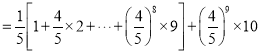
设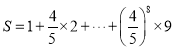 ,
,
则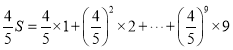 ,
,
两式作差得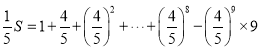
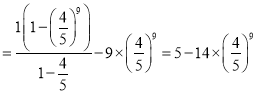 ,
,
![]()
![]() .
.

 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案