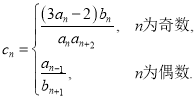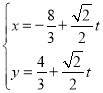题目内容
【题目】已知数列![]() 的首项a1=1,前n项和为Sn.设λ与k是常数,若对一切正整数n,均有
的首项a1=1,前n项和为Sn.设λ与k是常数,若对一切正整数n,均有![]() 成立,则称此数列为“λ~k”数列.
成立,则称此数列为“λ~k”数列.
(1)若等差数列![]() 是“λ~1”数列,求λ的值;
是“λ~1”数列,求λ的值;
(2)若数列![]() 是“
是“![]() ”数列,且an>0,求数列
”数列,且an>0,求数列![]() 的通项公式;
的通项公式;
(3)对于给定的λ,是否存在三个不同的数列![]() 为“λ~3”数列,且an≥0?若存在,求λ的取值范围;若不存在,说明理由,
为“λ~3”数列,且an≥0?若存在,求λ的取值范围;若不存在,说明理由,
【答案】(1)1
(2)![]()
(3)![]()
【解析】
(1)根据定义得![]() ,再根据和项与通项关系化简得
,再根据和项与通项关系化简得![]() ,最后根据数列不为零数列得结果;
,最后根据数列不为零数列得结果;
(2)根据定义得![]() ,根据平方差公式化简得
,根据平方差公式化简得![]() ,求得
,求得![]() ,即得
,即得![]() ;
;
(3)根据定义得![]() ,利用立方差公式化简得两个方程,再根据方程解的个数确定参数满足的条件,解得结果
,利用立方差公式化简得两个方程,再根据方程解的个数确定参数满足的条件,解得结果
(1)![]()
(2)![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
(3)假设存在三个不同的数列![]() 为
为![]() 数列.
数列.
![]()
![]() 或
或![]()
![]() 或
或![]()
∵对于给定的![]() ,存在三个不同的数列
,存在三个不同的数列![]() 为
为![]() 数列,且
数列,且![]()
![]() 或
或![]() 有两个不等的正根.
有两个不等的正根.
![]() 可转化为
可转化为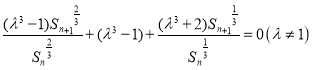 ,不妨设
,不妨设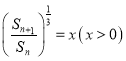 ,则
,则![]() 有两个不等正根,设
有两个不等正根,设![]() .
.
① 当![]() 时,
时,![]() ,即
,即![]() ,此时
,此时![]() ,
,![]() ,满足题意.
,满足题意.
② 当![]() 时,
时,![]() ,即
,即![]() ,此时
,此时![]() ,
,![]() ,此情况有两个不等负根,不满足题意舍去.
,此情况有两个不等负根,不满足题意舍去.
综上,![]()

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
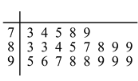
【题目】某学校课外兴趣小组利用假期到植物园开展社会实践活动,研究某种植物生长情况与温度的关系.现收集了该种植物月生长量y(cm)与月平均气温x(℃)的8组数据,并制成如图所示的散点图.
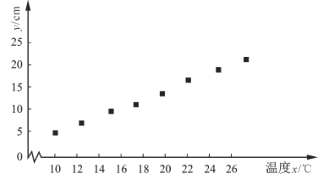
根据收集到的数据,计算得到如下值:
|
|
|
|
18 | 12.325 | 224.04 | 235.96 |
(1)求出y关于x的线性回归方程(最终结果的系数精确到0.01),并求温度为28℃时月生长量y的预报值;
(2)根据y关于x的回归方程,得到残差图如图所示,分析该回归方程的拟合效果.

附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ,
,![]() .
.